Archimedes

1.1. Thời thơ ấu và giáo dục

Archimedes sinh khoảng năm 287 TCN tại thành phố cảng Syracuse thuộc Sicilia, lúc bấy giờ là một thuộc địa tự trị trong vùng Magna Graecia. Ngày sinh của ông được xác định dựa trên ghi chép của học giả Hy Lạp Byzantine John Tzetzes, người khẳng định Archimedes sống 75 năm trước khi qua đời vào năm 212 TCN. Trong tác phẩm Người đếm cát, Archimedes nhắc đến cha mình là Phidias, một nhà thiên văn học mà không có thông tin chi tiết nào khác về ông. Plutarch trong cuốn Các cuộc đời song song của mình viết rằng Archimedes có quan hệ họ hàng với Hiero II, người cai trị Syracuse, mặc dù Cicero lại cho rằng ông xuất thân từ tầng lớp bình dân. Một cuốn tiểu sử về Archimedes đã được người bạn của ông là Heracleides viết, nhưng tác phẩm này đã bị thất lạc, khiến các chi tiết về cuộc đời ông trở nên mơ hồ. Ví dụ, không rõ liệu ông có kết hôn hay có con hay không, hoặc liệu ông có từng đến Alexandria ở Ai Cập trong thời niên thiếu hay không. Tuy nhiên, từ các tác phẩm còn sót lại của ông, rõ ràng ông duy trì mối quan hệ đồng nghiệp với các học giả ở đó, bao gồm người bạn Conon của Samos và thủ thư trưởng Eratosthenes. Trong lời tựa của tác phẩm Về các đường xoắn ốc gửi tới Dositheus của Pelusium, Archimedes có nhắc rằng "nhiều năm đã trôi qua kể từ cái chết của Conon," điều này cho thấy ông có thể đã lớn tuổi khi viết một số tác phẩm của mình.

1.2. Sự nghiệp

Các phiên bản tiêu chuẩn về cuộc đời Archimedes được các nhà sử học Hy Lạp và La Mã viết rất lâu sau khi ông qua đời. Tài liệu sớm nhất nhắc đến Archimedes xuất hiện trong Lịch sử của Polybius (khoảng 200-118 TCN), được viết khoảng 70 năm sau khi ông mất. Tác phẩm này ít làm sáng tỏ về con người Archimedes mà chủ yếu tập trung vào các máy chiến tranh mà ông được cho là đã chế tạo để bảo vệ thành phố khỏi người La Mã. Polybius ghi nhận rằng trong Chiến tranh Punic lần thứ hai, Syracuse đã chuyển lòng trung thành từ La Mã sang Carthage, dẫn đến một chiến dịch quân sự dưới sự chỉ huy của Marcus Claudius Marcellus và Appius Claudius Pulcher, những người đã vây hãm thành phố từ năm 213 đến 212 TCN. Ông lưu ý rằng người La Mã đã đánh giá thấp khả năng phòng thủ của Syracuse và đề cập đến một số cỗ máy do Archimedes thiết kế, bao gồm máy bắn đá cải tiến, các cỗ máy giống cần cẩu có thể xoay vòng cung, và các máy ném đá khác. Mặc dù cuối cùng người La Mã đã chiếm được thành phố, họ đã phải chịu tổn thất đáng kể do sự sáng tạo của Archimedes.

Cicero (106-43 TCN) cũng nhắc đến Archimedes trong một số tác phẩm của mình. Khi làm quan coi quốc khố ở Sicilia, Cicero đã tìm thấy cái mà ông cho là lăng mộ của Archimedes gần cổng Agrigentine ở Syracuse, trong tình trạng bị bỏ hoang và cây bụi phủ kín. Cicero đã cho dọn dẹp lăng mộ và có thể nhìn thấy hình khắc cùng đọc một số câu thơ được thêm vào làm bia ký. Lăng mộ có một bức tượng minh họa chứng minh toán học yêu thích của Archimedes, đó là thể tích và diện tích bề mặt của hình cầu bằng hai phần ba của hình trụ bao quanh nó, bao gồm cả các đáy. Cicero cũng đề cập rằng Marcellus đã mang về La Mã hai cung thiên văn do Archimedes chế tạo. Nhà sử học La Mã Livy (59 TCN-17 SCN) kể lại câu chuyện của Polybius về việc chiếm Syracuse và vai trò của Archimedes trong đó.

1.3. Cái chết

Plutarch (45-119 SCN) cung cấp ít nhất hai tài liệu về cách Archimedes qua đời sau khi Syracuse bị chiếm. Theo tài liệu phổ biến nhất, Archimedes đang suy ngẫm về một biểu đồ toán học khi thành phố bị chiếm. Một binh sĩ La Mã ra lệnh cho ông đến gặp Marcellus, nhưng ông từ chối, nói rằng ông phải hoàn thành công việc về vấn đề đó. Điều này khiến người lính tức giận, và anh ta đã giết Archimedes bằng thanh kiếm của mình. Một câu chuyện khác kể rằng Archimedes đang mang theo các dụng cụ toán học thì bị giết vì một người lính nghĩ rằng chúng là những vật có giá trị. Marcellus được cho là đã tức giận vì cái chết của Archimedes, vì ông coi ông là một tài sản khoa học quý giá (ông gọi Archimedes là "một Briareus hình học") và đã ra lệnh rằng ông không được làm hại.

Những lời cuối cùng được cho là của Archimedes là "Đừng làm hỏng các hình tròn của ta" (Noli turbare circulos meos^Latin; μὴ μου τοὺς κύkλους τάραττε^{Greek, Modern}), ám chỉ đến bản vẽ toán học mà ông được cho là đang nghiên cứu khi bị người lính La Mã làm phiền. Không có bằng chứng đáng tin cậy nào cho thấy Archimedes đã nói những lời này và chúng không xuất hiện trong tài liệu của Plutarch. Một câu trích dẫn tương tự được tìm thấy trong tác phẩm của Valerius Maximus (khoảng 30 SCN), người đã viết trong Những việc làm và lời nói đáng nhớ, "

... sed protecto manibus puluere 'noli' inquit, 'obsecro, istum disturbare'

2.1. Phương pháp loại trừ và Vô cùng nhỏ

Archimedes đã có thể sử dụng các khái niệm về vô cùng nhỏ (tiền thân của vi phân) theo cách tương tự như tính toán tích phân hiện đại. Thông qua chứng minh bằng phản chứng (reductio ad absurdum), ông có thể đưa ra câu trả lời cho các bài toán với một mức độ chính xác tùy ý, đồng thời xác định các giới hạn mà câu trả lời nằm trong đó. Kỹ thuật này được gọi là phương pháp vét cạn, và ông đã sử dụng nó để ước tính diện tích của các hình và giá trị của π.

2.2. Tính toán số Pi

Trong tác phẩm Đo đạc một hình tròn, ông đã thực hiện điều này bằng cách vẽ một đa giác đều lớn hơn bên ngoài một hình tròn và sau đó một đa giác đều nhỏ hơn bên trong hình tròn, và liên tục nhân đôi số cạnh của mỗi đa giác đều, tính toán độ dài cạnh của mỗi đa giác ở mỗi bước. Khi số cạnh tăng lên, nó trở thành một ước lượng chính xác hơn của một hình tròn. Sau bốn bước như vậy, khi các đa giác có 96 cạnh, ông đã có thể xác định rằng giá trị của π nằm trong khoảng từ 3 và 1/7 (khoảng 3.1429) đến 3 và 10/71 (khoảng 3.1408), phù hợp với giá trị thực của nó là khoảng 3.1416. Ông cũng chứng minh rằng diện tích hình tròn bằng π nhân với bình phương của bán kính hình tròn (πr²).

2.3. Hình học

Trong tác phẩm Phép cầu phương hình parabol, Archimedes đã chứng minh rằng diện tích được bao bởi một đường parabol và một đường thẳng bằng 4/3 lần diện tích của một hình tam giác nội tiếp tương ứng như trong hình bên phải. Ông đã thể hiện lời giải cho vấn đề này dưới dạng tổng của chuỗi hình học vô hạn 1 + 4^-1 + 4^-2 + 4^-3 + ... với tỷ lệ chung là 1/4, có tổng là 4/3.
Nếu số hạng đầu tiên trong chuỗi này là diện tích của tam giác, thì số hạng thứ hai là tổng diện tích của hai tam giác có đáy là hai đường cát tuyến nhỏ hơn, và đỉnh thứ ba của chúng là nơi đường thẳng song song với trục của parabol và đi qua trung điểm của đáy cắt parabol, và cứ thế tiếp tục. Chứng minh này sử dụng một biến thể của chuỗi 1/4 + 1/16 + 1/64 + 1/256 + ... có tổng là 1/3.

Trong tác phẩm Về hình cầu và hình trụ, Archimedes đã đạt được kết quả mà ông tự hào nhất, đó là mối quan hệ giữa một hình cầu và một hình trụ ngoại tiếp có cùng chiều cao và đường kính. Thể tích của hình cầu là 4/3πr³ và của hình trụ là 2πr³. Diện tích bề mặt của hình cầu là 4πr² và của hình trụ là 6πr² (bao gồm hai đáy), trong đó r là bán kính của hình cầu và hình trụ.

Trong Về các hình nêm và hình cầu, một tác phẩm gồm 32 mệnh đề gửi Dositheus, Archimedes tính toán diện tích và thể tích của các mặt cắt của hình nón, hình cầu và paraboloid.

2.4. Tính chất Archimedes

Trong Về hình cầu và hình trụ, Archimedes đặt ra tiên đề rằng bất kỳ đại lượng nào khi được cộng với chính nó đủ số lần sẽ vượt quá bất kỳ đại lượng nào cho trước. Ngày nay, điều này được gọi là tính chất Archimedes của số thực.

Trong Đo đạc một hình tròn, Archimedes đưa ra giá trị của căn bậc hai của 3 nằm giữa 265/153 (khoảng 1.7320261) và 1351/780 (khoảng 1.7320512). Giá trị thực là khoảng 1.7320508, khiến đây là một ước lượng rất chính xác. Ông đưa ra kết quả này mà không giải thích cách ông đạt được nó. Khía cạnh này trong công trình của Archimedes đã khiến John Wallis nhận xét rằng ông: "như thể cố ý che giấu dấu vết của cuộc điều tra của mình, như thể ông tiếc nuối hậu thế bí mật về phương pháp tìm kiếm của mình trong khi ông muốn buộc họ phải đồng ý với kết quả của ông." Có thể ông đã sử dụng một quy trình lặp lại để tính toán các giá trị này.

2.5. Người đếm cát

Trong tác phẩm Người đếm cát, Archimedes đã đặt ra mục tiêu tính toán một con số lớn hơn số hạt cát cần thiết để lấp đầy vũ trụ. Khi làm như vậy, ông đã thách thức quan niệm rằng số lượng hạt cát quá lớn để có thể đếm được. Ông viết:

Có một số người, Vua Gelo, nghĩ rằng số lượng hạt cát là vô hạn; và tôi muốn nói đến cát không chỉ là những gì tồn tại quanh Syracuse và phần còn lại của Sicilia mà còn là những gì được tìm thấy ở mọi vùng, dù có người ở hay không.

2.6. Các tác phẩm toán học chính

Các tác phẩm toán học quan trọng còn sót lại của ông bao gồm:

• Đo đạc một hình tròn: Đây là một tác phẩm ngắn gồm ba mệnh đề, được viết dưới dạng thư từ với Dositheus của Pelusium. Trong Mệnh đề II, Archimedes đưa ra một ước lượng giá trị của số Pi (π), cho thấy nó lớn hơn 223/71 (khoảng 3.1408...) và nhỏ hơn 22/7 (khoảng 3.1428...).
• Người đếm cát: Trong chuyên luận này, còn được gọi là Psammites, Archimedes tìm ra một con số lớn hơn số hạt cát cần thiết để lấp đầy vũ trụ. Cuốn sách này đề cập đến thuyết nhật tâm của Hệ Mặt Trời do Aristarchus của Samos đề xuất, cũng như các ý tưởng đương thời về kích thước của Trái Đất và khoảng cách giữa các thiên thể khác nhau, và cố gắng đo đường kính biểu kiến của Mặt Trời. Bằng cách sử dụng một hệ thống số dựa trên lũy thừa của myriad, Archimedes kết luận rằng số hạt cát cần thiết để lấp đầy vũ trụ là 8 x 10⁶³ trong ký hiệu hiện đại. Lá thư mở đầu cho biết cha của Archimedes là một nhà thiên văn học tên là Phidias. Người đếm cát là tác phẩm duy nhất còn sót lại trong đó Archimedes thảo luận về quan điểm của mình về thiên văn học.
• Về sự cân bằng của các hành tinh: Tác phẩm này gồm hai cuốn. Cuốn thứ nhất chứa bảy tiên đề và mười lăm mệnh đề, trong khi cuốn thứ hai chứa mười mệnh đề. Trong cuốn thứ nhất, Archimedes chứng minh định luật đòn bẩy, phát biểu rằng:

Các đại lượng cân bằng ở những khoảng cách tỷ lệ nghịch với trọng lượng của chúng.

• Phép cầu phương hình parabol: Trong tác phẩm gồm 24 mệnh đề gửi Dositheus này, Archimedes chứng minh bằng hai phương pháp rằng diện tích được bao bởi một đường parabol và một đường thẳng bằng 4/3 diện tích của một hình tam giác có cùng đáy và chiều cao. Ông đạt được điều này trong một trong các chứng minh của mình bằng cách tính toán giá trị của một chuỗi hình học có tổng vô hạn với tỷ lệ 1/4.
• Về hình cầu và hình trụ: Trong chuyên luận hai tập này gửi Dositheus, Archimedes đạt được kết quả mà ông tự hào nhất, đó là mối quan hệ giữa một hình cầu và một hình trụ ngoại tiếp có cùng chiều cao và đường kính. Thể tích là 4/3πr³ đối với hình cầu, và 2πr³ đối với hình trụ. Diện tích bề mặt là 4πr² đối với hình cầu, và 6πr² đối với hình trụ (bao gồm hai đáy), trong đó r là bán kính của hình cầu và hình trụ.
• Về các đường xoắn ốc: Tác phẩm gồm 28 mệnh đề này cũng gửi Dositheus. Chuyên luận định nghĩa cái mà ngày nay được gọi là xoắn ốc Archimedes. Nó là quỹ tích của các điểm tương ứng với các vị trí theo thời gian của một điểm di chuyển ra khỏi một điểm cố định với tốc độ không đổi dọc theo một đường thẳng quay với vận tốc góc không đổi. Tương đương, trong hệ tọa độ cực (r, θ), nó có thể được mô tả bằng phương trình r = a + bθ với các số thực a và b. Đây là một ví dụ ban đầu về một đường cong cơ học (một đường cong được vẽ bởi một điểm chuyển động) được một nhà toán học Hy Lạp xem xét.
• Về các hình nêm và hình cầu: Đây là một tác phẩm gồm 32 mệnh đề gửi Dositheus. Trong chuyên luận này, Archimedes tính toán diện tích và thể tích của các mặt cắt của hình nón, hình cầu và paraboloid.
• Về các vật thể nổi: Tác phẩm này gồm hai cuốn. Trong cuốn thứ nhất, Archimedes trình bày định luật cân bằng của chất lỏng và chứng minh rằng nước sẽ có hình cầu quanh một tâm khối lượng. Điều này có thể là một nỗ lực nhằm giải thích lý thuyết của các nhà thiên văn học Hy Lạp đương thời như Eratosthenes rằng Trái Đất hình tròn. Các chất lỏng được Archimedes mô tả không tự hấp dẫn vì ông giả định sự tồn tại của một điểm mà mọi vật đều rơi về phía đó để suy ra hình cầu.

Trong phần thứ hai, ông tính toán các vị trí cân bằng của các phần paraboloid. Đây có lẽ là một sự lý tưởng hóa hình dạng của thân tàu. Một số phần của ông nổi với đáy dưới nước và đỉnh trên mặt nước, tương tự như cách các núi băng nổi. Nguyên lý Archimedes về sức nổi được đưa ra trong tác phẩm này, được phát biểu như sau:

Bất kỳ vật thể nào ngập hoàn toàn hoặc một phần trong chất lỏng đều chịu một lực đẩy lên bằng, nhưng ngược chiều với, trọng lượng của chất lỏng bị thay thế.

• Ostomachion: Còn được gọi là Loculus của Archimedes hoặc Hộp Archimedes, đây là một câu đố cắt ghép tương tự như Tangram, và chuyên luận mô tả nó được tìm thấy ở dạng hoàn chỉnh hơn trong Sách da cừu Archimedes. Archimedes tính toán diện tích của 14 mảnh có thể được lắp ráp để tạo thành một hình vuông. Reviel Netz của Đại học Stanford đã lập luận vào năm 2003 rằng Archimedes đang cố gắng xác định có bao nhiêu cách các mảnh có thể được lắp ráp thành hình vuông. Netz tính toán rằng các mảnh có thể được tạo thành hình vuông theo 17.152 cách. Số lượng cách sắp xếp là 536 khi các giải pháp tương đương bằng cách xoay và phản chiếu bị loại trừ. Câu đố này đại diện cho một ví dụ về một vấn đề ban đầu trong tổ hợp. Nguồn gốc tên của câu đố không rõ ràng, và đã có gợi ý rằng nó được lấy từ từ tiếng Hy Lạp cổ đại có nghĩa là "cổ họng" hoặc "thực quản", stomachos (στόμαχος^{Greek, Ancient}). Ausonius gọi câu đố là Ostomachion, một từ ghép tiếng Hy Lạp được hình thành từ gốc của osteon_ostéon^{Greek, Ancient} (xương) và machē_mákhē^{Greek, Ancient} (chiến đấu).
• Bài toán đàn gia súc Archimedes: Gotthold Ephraim Lessing đã khám phá ra tác phẩm này trong một bản thảo tiếng Hy Lạp bao gồm một bài thơ 44 dòng tại Thư viện Herzog August ở Wolfenbüttel, Đức vào năm 1773. Nó được gửi đến Eratosthenes và các nhà toán học ở Alexandria. Archimedes thách thức họ đếm số lượng gia súc trong Đàn gia súc của Mặt Trời bằng cách giải một số phương trình Diophantine đồng thời. Có một phiên bản khó hơn của bài toán trong đó một số câu trả lời được yêu cầu phải là số chính phương. A. Amthor đã giải phiên bản này của bài toán lần đầu tiên vào năm 1880, và câu trả lời là một số rất lớn, khoảng 7.760271 x 10²⁰⁶⁵⁴⁴.
• Phương pháp Định lý Cơ học: Chuyên luận này được cho là đã mất cho đến khi Sách da cừu Archimedes được phát hiện vào năm 1906. Trong tác phẩm này, Archimedes sử dụng các vô cùng nhỏ, và cho thấy cách chia một hình thành vô số phần vô cùng nhỏ có thể được sử dụng để xác định diện tích hoặc thể tích của nó. Ông có thể đã coi phương pháp này thiếu sự chặt chẽ về mặt hình thức, vì vậy ông cũng sử dụng phương pháp vét cạn để suy ra các kết quả. Giống như Bài toán đàn gia súc Archimedes, Phương pháp Định lý Cơ học được viết dưới dạng một lá thư gửi cho Eratosthenes ở Alexandria.

3.1. Nguyên lý sức nổi

Giai thoại nổi tiếng nhất về Archimedes kể về cách ông phát minh ra một phương pháp để xác định thể tích của một vật thể có hình dạng không đều. Theo Vitruvius, một chiếc vương miện cho một ngôi đền đã được làm cho Vua Hiero II của Syracuse, người đã cung cấp vàng nguyên chất để sử dụng. Chiếc vương miện có lẽ được làm theo hình dạng một vòng nguyệt quế. Archimedes được yêu cầu xác định xem thợ kim hoàn có thay thế một phần bạc mà không làm hỏng vương miện hay không, vì vậy ông không thể nấu chảy nó thành một vật thể có hình dạng đều đặn để tính mật độ của nó.

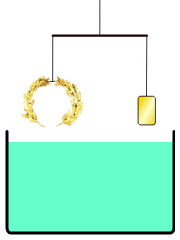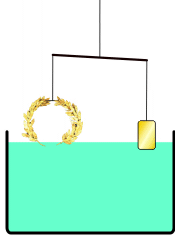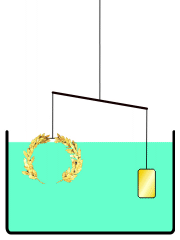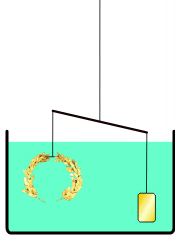
Trong câu chuyện này, Archimedes nhận thấy khi đang tắm rằng mực nước trong bồn tăng lên khi ông bước vào, và nhận ra rằng hiệu ứng này có thể được sử dụng để xác định thể tích của vương miện vàng. Archimedes quá phấn khích với khám phá này đến nỗi ông chạy ra đường trong tình trạng khỏa thân, quên cả mặc quần áo, la lên "Eureka!" (εὕρηκα^{Greek, Modern}, heúrēka!, nghĩa là "Tôi đã tìm ra rồi!"). Vì mục đích thực tế, nước không nén được, nên chiếc vương miện bị nhấn chìm sẽ dịch chuyển một lượng nước bằng thể tích của nó. Bằng cách chia khối lượng của vương miện cho thể tích nước bị dịch chuyển, có thể thu được mật độ của nó; nếu các kim loại rẻ hơn và ít đặc hơn đã được thêm vào, mật độ sẽ thấp hơn mật độ của vàng. Archimedes phát hiện ra rằng điều này đã xảy ra, chứng minh rằng bạc đã được trộn vào.

Câu chuyện về vương miện vàng không xuất hiện trong bất kỳ tác phẩm nào đã biết của Archimedes. Tính thực tế của phương pháp được mô tả đã bị nghi ngờ do độ chính xác cực cao cần thiết để đo sự dịch chuyển của chất lỏng. Archimedes có thể thay vào đó đã tìm kiếm một giải pháp áp dụng nguyên lý thủy tĩnh học được gọi là nguyên lý Archimedes, được tìm thấy trong chuyên luận Về các vật thể nổi của ông: một vật thể nhúng trong chất lỏng sẽ chịu một lực nổi bằng trọng lượng của chất lỏng mà nó dịch chuyển. Sử dụng nguyên lý này, có thể so sánh mật độ của vương miện với mật độ của vàng nguyên chất bằng cách cân nó trên một cái cân với một mẫu vàng nguyên chất cùng trọng lượng, sau đó nhúng thiết bị vào nước. Sự khác biệt về mật độ giữa hai mẫu sẽ làm cho cân nghiêng tương ứng. Galileo Galilei, người đã phát minh ra một cân thủy tĩnh vào năm 1586 lấy cảm hứng từ công trình của Archimedes, coi đó là "có khả năng phương pháp này giống với phương pháp mà Archimedes đã theo, vì, ngoài việc rất chính xác, nó dựa trên những chứng minh do chính Archimedes tìm thấy."

3.2. Định luật Đòn bẩy

Mặc dù Archimedes không phát minh ra đòn bẩy, ông đã đưa ra một chứng minh toán học về nguyên lý liên quan trong tác phẩm Về sự cân bằng của các hành tinh. Các mô tả trước đó về nguyên lý đòn bẩy được tìm thấy trong một tác phẩm của Euclid và trong Các vấn đề Cơ học, thuộc trường phái Peripatetic của những người theo Aristotle, mà quyền tác giả của nó đã được một số người gán cho Archytas.

Có một số báo cáo, thường mâu thuẫn, về những kỳ công của Archimedes khi sử dụng đòn bẩy để nâng các vật rất nặng. Plutarch mô tả cách Archimedes thiết kế hệ thống ròng rọc phức hợp, cho phép các thủy thủ sử dụng nguyên lý lợi thế cơ học để nâng các vật mà nếu không thì quá nặng để di chuyển. Theo Pappus của Alexandria, công trình của Archimedes về đòn bẩy và sự hiểu biết của ông về lợi thế cơ học đã khiến ông nhận xét: "Hãy cho tôi một điểm tựa, và tôi sẽ nhấc bổng cả Trái Đất" (δῶς μοι πᾶ στῶ καὶ τὰν γᾶν κινάσω^{Greek, Modern}). Olympiodorus Trẻ sau này gán cùng lời khoe khoang đó cho phát minh baroulkos của Archimedes, một loại tời, chứ không phải đòn bẩy.

3.3. Tĩnh học và Thủy tĩnh học

Archimedes đã có những đóng góp đáng kể trong lĩnh vực tĩnh học và thủy tĩnh học. Ông không chỉ chứng minh định luật đòn bẩy mà còn sử dụng rộng rãi khái niệm tâm khối lượng trong các công trình của mình.

3.4. Phát minh

Archimedes đã mô tả chi tiết các phát minh và thiết bị cơ khí đa dạng của mình.

3.4.1. Máy bơm trục vít (Vít Archimedes)

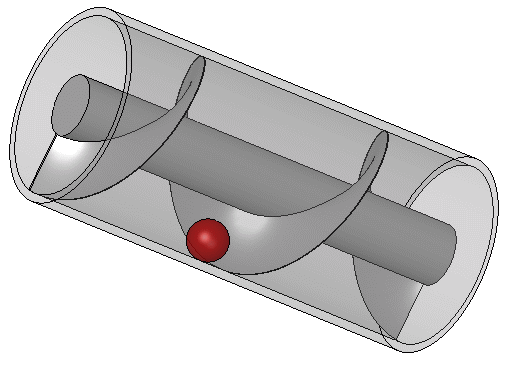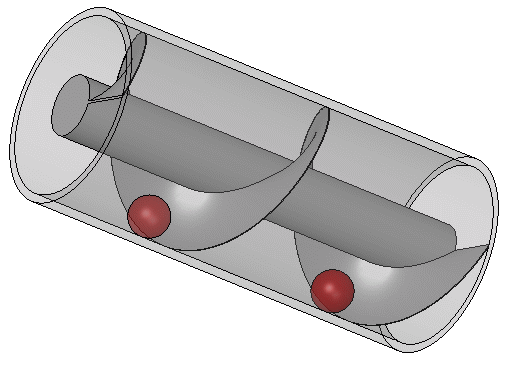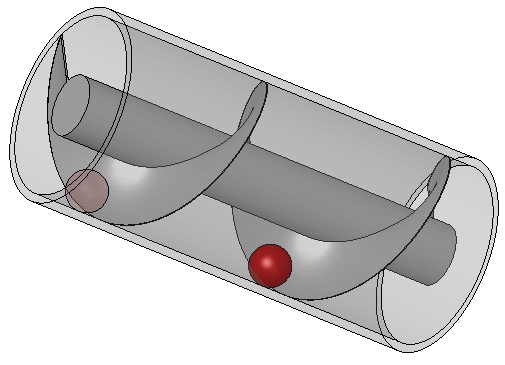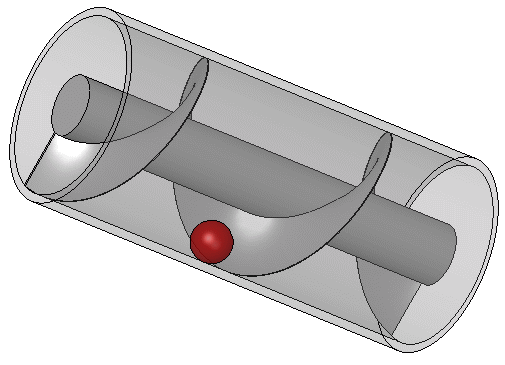
Một phần lớn công trình của Archimedes trong kỹ thuật có lẽ phát sinh từ việc đáp ứng nhu cầu của quê hương ông là Syracuse. Athenaeus của Naucratis trích dẫn một Moschion nào đó trong một mô tả về việc Vua Hiero II đã đặt hàng thiết kế một con tàu khổng lồ, chiếc Syracusia, có thể được sử dụng để du lịch sang trọng, chở hàng tiếp tế và làm biểu tượng của sức mạnh hải quân. Syracusia được cho là con tàu lớn nhất được đóng trong thời cổ đại và, theo lời kể của Moschion, nó đã được Archimedes hạ thủy. Con tàu này có lẽ có khả năng chở 600 người và bao gồm các khu vườn trang trí, một phòng tập thể dục, và một ngôi đền dành riêng cho nữ thần Aphrodite trong số các tiện nghi của nó. Tài liệu cũng đề cập rằng, để loại bỏ bất kỳ lượng nước tiềm năng nào rò rỉ qua thân tàu, một thiết bị có lưỡi xoắn ốc quay bên trong một hình trụ đã được Archimedes thiết kế.

Vít Archimedes được quay bằng tay, và cũng có thể được sử dụng để chuyển nước từ một vùng nước thấp lên các kênh thủy lợi. Vít vẫn được sử dụng ngày nay để bơm chất lỏng và chất rắn dạng hạt như than và ngũ cốc. Được mô tả bởi Vitruvius, thiết bị của Archimedes có thể là một cải tiến so với một máy bơm trục vít đã được sử dụng để tưới tiêu cho Vườn treo Babylon. Con tàu hơi nước đầu tiên trên thế giới có chân vịt là SS Archimedes, được hạ thủy vào năm 1839 và được đặt tên để vinh danh Archimedes và công trình của ông về vít.

3.4.3. Tia chiếu nhiệt huyền thoại

Theo truyền thuyết, Archimedes đã sắp xếp các gương như một thiết bị phản xạ parabol để đốt cháy các tàu tấn công Syracuse bằng cách tập trung ánh sáng mặt trời. Mặc dù không có bằng chứng đương đại nào về kỳ công này và các học giả hiện đại tin rằng nó không xảy ra, Archimedes có thể đã viết một tác phẩm về gương có tựa đề Catoptrica. Lucian và Galen, viết vào thế kỷ thứ hai SCN, đã đề cập rằng trong cuộc vây hãm Syracuse, Archimedes đã đốt cháy các tàu địch. Gần bốn trăm năm sau, Anthemius của Tralles, mặc dù hoài nghi, đã cố gắng tái tạo hình học phản xạ giả thuyết của Archimedes.

Thiết bị được cho là, đôi khi được gọi là "tia chiếu nhiệt Archimedes", đã là chủ đề của một cuộc tranh luận liên tục về độ tin cậy của nó kể từ thời Phục Hưng. René Descartes đã bác bỏ nó là sai, trong khi các nhà nghiên cứu hiện đại đã cố gắng tái tạo hiệu ứng này chỉ bằng các phương tiện có sẵn cho Archimedes, chủ yếu với kết quả tiêu cực. Người ta đã gợi ý rằng một mảng lớn các tấm chắn đồng thau hoặc đồng được đánh bóng cao hoạt động như gương có thể đã được sử dụng để tập trung ánh sáng mặt trời vào một con tàu, nhưng hiệu ứng tổng thể sẽ là làm chói mắt, làm lóa mắt, hoặc làm phân tâm thủy thủ đoàn của con tàu hơn là gây cháy. Sử dụng vật liệu hiện đại và quy mô lớn hơn, các lò mặt trời tập trung ánh sáng mặt trời có thể đạt nhiệt độ rất cao, và đôi khi được sử dụng để tạo ra điện.

4.1. Các tác phẩm còn tồn tại

Các tác phẩm sau đây được sắp xếp theo thứ tự thời gian dựa trên các tiêu chí thuật ngữ và lịch sử mới do Knorr (1978) và Sato (1986) đặt ra.

• Đo đạc một hình tròn: Đây là một tác phẩm ngắn gồm ba mệnh đề. Nó được viết dưới dạng thư từ với Dositheus của Pelusium, người là học trò của Conon của Samos. Trong Mệnh đề II, Archimedes đưa ra một ước lượng giá trị của số Pi (π), cho thấy nó lớn hơn 223/71 (3.1408...) và nhỏ hơn 22/7 (3.1428...).
• Người đếm cát: Trong chuyên luận này, còn được gọi là Psammites, Archimedes tìm ra một con số lớn hơn số hạt cát cần thiết để lấp đầy vũ trụ. Cuốn sách này đề cập đến thuyết nhật tâm của Hệ Mặt Trời do Aristarchus của Samos đề xuất, cũng như các ý tưởng đương thời về kích thước của Trái Đất và khoảng cách giữa các thiên thể khác nhau, và cố gắng đo đường kính biểu kiến của Mặt Trời. Bằng cách sử dụng một hệ thống số dựa trên lũy thừa của myriad, Archimedes kết luận rằng số hạt cát cần thiết để lấp đầy vũ trụ là 8 x 10⁶³ trong ký hiệu hiện đại. Lá thư mở đầu cho biết cha của Archimedes là một nhà thiên văn học tên là Phidias. Người đếm cát là tác phẩm duy nhất còn sót lại trong đó Archimedes thảo luận về quan điểm của mình về thiên văn học.
• Về sự cân bằng của các hành tinh: Tác phẩm này gồm hai cuốn: cuốn thứ nhất chứa bảy tiên đề và mười lăm mệnh đề, trong khi cuốn thứ hai chứa mười mệnh đề. Trong cuốn thứ nhất, Archimedes chứng minh định luật đòn bẩy, phát biểu rằng:

Các đại lượng cân bằng ở những khoảng cách tỷ lệ nghịch với trọng lượng của chúng.

• Phép cầu phương hình parabol: Trong tác phẩm gồm 24 mệnh đề gửi Dositheus này, Archimedes chứng minh bằng hai phương pháp rằng diện tích được bao bởi một đường parabol và một đường thẳng bằng 4/3 diện tích của một hình tam giác có cùng đáy và chiều cao. Ông đạt được điều này trong một trong các chứng minh của mình bằng cách tính toán giá trị của một chuỗi hình học có tổng vô hạn với tỷ lệ 1/4.
• Về hình cầu và hình trụ: Trong chuyên luận hai tập này gửi Dositheus, Archimedes đạt được kết quả mà ông tự hào nhất, đó là mối quan hệ giữa một hình cầu và một hình trụ ngoại tiếp có cùng chiều cao và đường kính. Thể tích là 4/3πr³ đối với hình cầu, và 2πr³ đối với hình trụ. Diện tích bề mặt là 4πr² đối với hình cầu, và 6πr² đối với hình trụ (bao gồm hai đáy), trong đó r là bán kính của hình cầu và hình trụ.
• Về các đường xoắn ốc: Tác phẩm gồm 28 mệnh đề này cũng gửi Dositheus. Chuyên luận định nghĩa cái mà ngày nay được gọi là xoắn ốc Archimedes. Nó là quỹ tích của các điểm tương ứng với các vị trí theo thời gian của một điểm di chuyển ra khỏi một điểm cố định với tốc độ không đổi dọc theo một đường thẳng quay với vận tốc góc không đổi. Tương đương, trong hệ tọa độ cực (r, θ), nó có thể được mô tả bằng phương trình r = a + bθ với các số thực a và b. Đây là một ví dụ ban đầu về một đường cong cơ học (một đường cong được vẽ bởi một điểm chuyển động) được một nhà toán học Hy Lạp xem xét.
• Về các hình nêm và hình cầu: Đây là một tác phẩm gồm 32 mệnh đề gửi Dositheus. Trong chuyên luận này, Archimedes tính toán diện tích và thể tích của các mặt cắt của hình nón, hình cầu và paraboloid.
• Về các vật thể nổi: Tác phẩm này gồm hai cuốn. Trong cuốn thứ nhất, Archimedes trình bày định luật cân bằng của chất lỏng và chứng minh rằng nước sẽ có hình cầu quanh một tâm khối lượng. Điều này có thể là một nỗ lực nhằm giải thích lý thuyết của các nhà thiên văn học Hy Lạp đương thời như Eratosthenes rằng Trái Đất hình tròn. Các chất lỏng được Archimedes mô tả không tự hấp dẫn vì ông giả định sự tồn tại của một điểm mà mọi vật đều rơi về phía đó để suy ra hình cầu.

Trong phần thứ hai, ông tính toán các vị trí cân bằng của các phần paraboloid. Đây có lẽ là một sự lý tưởng hóa hình dạng của thân tàu. Một số phần của ông nổi với đáy dưới nước và đỉnh trên mặt nước, tương tự như cách các núi băng nổi. Nguyên lý Archimedes về sức nổi được đưa ra trong tác phẩm này, được phát biểu như sau:

Bất kỳ vật thể nào ngập hoàn toàn hoặc một phần trong chất lỏng đều chịu một lực đẩy lên bằng, nhưng ngược chiều với, trọng lượng của chất lỏng bị thay thế.

• Ostomachion: Còn được gọi là Loculus của Archimedes hoặc Hộp Archimedes, đây là một câu đố cắt ghép tương tự như Tangram, và chuyên luận mô tả nó được tìm thấy ở dạng hoàn chỉnh hơn trong Sách da cừu Archimedes. Archimedes tính toán diện tích của 14 mảnh có thể được lắp ráp để tạo thành một hình vuông. Reviel Netz của Đại học Stanford đã lập luận vào năm 2003 rằng Archimedes đang cố gắng xác định có bao nhiêu cách các mảnh có thể được lắp ráp thành hình vuông. Netz tính toán rằng các mảnh có thể được tạo thành hình vuông theo 17.152 cách. Số lượng cách sắp xếp là 536 khi các giải pháp tương đương bằng cách xoay và phản chiếu bị loại trừ. Câu đố này đại diện cho một ví dụ về một vấn đề ban đầu trong tổ hợp. Nguồn gốc tên của câu đố không rõ ràng, và đã có gợi ý rằng nó được lấy từ từ tiếng Hy Lạp cổ đại có nghĩa là "cổ họng" hoặc "thực quản", stomachos (στόμαχος^{Greek, Ancient}). Ausonius gọi câu đố là Ostomachion, một từ ghép tiếng Hy Lạp được hình thành từ gốc của osteon_ostéon^{Greek, Ancient} (xương) và machē_mákhē^{Greek, Ancient} (chiến đấu).
• Bài toán đàn gia súc Archimedes: Gotthold Ephraim Lessing đã khám phá ra tác phẩm này trong một bản thảo tiếng Hy Lạp bao gồm một bài thơ 44 dòng tại Thư viện Herzog August ở Wolfenbüttel, Đức vào năm 1773. Nó được gửi đến Eratosthenes và các nhà toán học ở Alexandria. Archimedes thách thức họ đếm số lượng gia súc trong Đàn gia súc của Mặt Trời bằng cách giải một số phương trình Diophantine đồng thời. Có một phiên bản khó hơn của bài toán trong đó một số câu trả lời được yêu cầu phải là các số chính phương. A. Amthor đã giải phiên bản này của bài toán lần đầu tiên vào năm 1880, và câu trả lời là một số rất lớn, khoảng 7.760271 x 10²⁰⁶⁵⁴⁴.
• Phương pháp Định lý Cơ học: Chuyên luận này được cho là đã mất cho đến khi Sách da cừu Archimedes được phát hiện vào năm 1906. Trong tác phẩm này, Archimedes sử dụng các vô cùng nhỏ, và cho thấy cách chia một hình thành vô số phần vô cùng nhỏ có thể được sử dụng để xác định diện tích hoặc thể tích của nó. Ông có thể đã coi phương pháp này thiếu sự chặt chẽ về mặt hình thức, vì vậy ông cũng sử dụng phương pháp vét cạn để suy ra các kết quả. Giống như Bài toán đàn gia súc Archimedes, Phương pháp Định lý Cơ học được viết dưới dạng một lá thư gửi cho Eratosthenes ở Alexandria.

4.2. Các tác phẩm đã mất

Các tác phẩm của Archimedes chỉ được biết đến thông qua các ghi chép của các tác giả cổ đại khác bao gồm:

• Về việc chế tạo hình cầu và một tác phẩm về đa diện được nhắc đến bởi Pappus của Alexandria.
• Catoptrica, một tác phẩm về quang học được nhắc đến bởi Theon của Alexandria.
• Các định lý, gửi tới Zeuxippus và giải thích hệ thống số được dùng trong Người đếm cát.
• Về những sự cân bằng và đòn bẩy.
• Về các trung tâm trọng lực.
• Về lịch.

4.3. Sách da cừu Archimedes

Tài liệu quan trọng nhất chứa đựng công trình của Archimedes là Sách da cừu Archimedes. Năm 1906, giáo sư người Đan Mạch Johan Ludvig Heiberg đã đến thăm Constantinople để kiểm tra một giấy da da dê 174 trang của các bài kinh, được viết vào thế kỷ 13, sau khi đọc một bản sao ngắn được xuất bản bảy năm trước đó bởi Athanasios Papadopoulos-Kerameus. Ông xác nhận rằng đó thực sự là một palimpsest, một tài liệu có văn bản đã được viết lại trên một tác phẩm cũ bị xóa. Palimpsest được tạo ra bằng cách cạo mực từ các tác phẩm hiện có và tái sử dụng chúng, một thực hành phổ biến trong thời Trung Cổ, vì giấy da rất đắt. Các tác phẩm cũ hơn trong palimpsest được các học giả xác định là các bản sao thế kỷ 10 của các chuyên luận bị thất lạc trước đây của Archimedes. Cuốn giấy da này đã trải qua hàng trăm năm trong thư viện tu viện ở Constantinople trước khi được bán cho một nhà sưu tập tư nhân vào những năm 1920. Vào ngày 29 tháng 10 năm 1998, nó đã được bán đấu giá cho một người mua ẩn danh với tổng giá trị 2.20 M USD.

Cuốn palimpsest chứa bảy chuyên luận, bao gồm bản sao duy nhất còn sót lại của Về các vật thể nổi bằng tiếng Hy Lạp gốc. Đây là nguồn duy nhất được biết đến của Phương pháp Định lý Cơ học, được Suda nhắc đến và tưởng chừng đã bị thất lạc vĩnh viễn. Ostomachion cũng được phát hiện trong palimpsest, với một phân tích hoàn chỉnh hơn về câu đố so với những gì đã được tìm thấy trong các văn bản trước đây. Cuốn palimpsest được lưu giữ tại Bảo tàng Nghệ thuật Walters ở Baltimore, Maryland, nơi nó đã được kiểm tra bằng một loạt các thử nghiệm hiện đại bao gồm việc sử dụng tia cực tím và tia X để đọc văn bản bị ghi đè. Kể từ đó, nó đã trở lại với chủ sở hữu ẩn danh của nó.

Các chuyên luận trong Sách da cừu Archimedes bao gồm:

• Về sự cân bằng của các hành tinh
• Về các đường xoắn ốc
• Đo đạc một hình tròn
• Về hình cầu và hình trụ
• Về các vật thể nổi
• Phương pháp Định lý Cơ học
• Ostomachion
• Các bài diễn văn của chính trị gia thế kỷ 4 TCN Hypereides
• Một bình luận về Thể loại của Aristotle
• Các tác phẩm khác

5.1. Ảnh hưởng đến Toán học và Vật lý

Các nhà sử học khoa học và toán học gần như đồng ý rằng Archimedes là nhà toán học xuất sắc nhất từ thời cổ đại. Eric Temple Bell, ví dụ, đã viết:

Bất kỳ danh sách nào về ba nhà toán học "vĩ đại nhất" trong lịch sử sẽ bao gồm tên của Archimedes. Hai người còn lại thường được liên kết với ông là Isaac Newton và Carl Friedrich Gauss. Một số người, xem xét sự giàu có-hoặc nghèo nàn-tương đối của toán học và khoa học vật lý trong các thời đại tương ứng mà những người khổng lồ này sống, và đánh giá thành tựu của họ trong bối cảnh thời đại của họ, sẽ đặt Archimedes lên hàng đầu.

... vào năm 1500, châu Âu biết ít hơn Archimedes, người đã qua đời vào năm 212 TCN ...

Nếu chúng ta xem xét những gì tất cả những người khác đã đạt được trong toán học và vật lý, trên mọi lục địa và trong mọi nền văn minh, từ đầu thời gian cho đến thế kỷ 17 ở Tây Âu, những thành tựu của Archimedes vượt xa tất cả. Ông là một nền văn minh vĩ đại tự thân.

Và vì vậy, vì Archimedes đã dẫn dắt hơn bất kỳ ai khác đến sự hình thành của giải tích và vì ông là người tiên phong trong việc ứng dụng toán học vào thế giới vật lý, hóa ra khoa học phương Tây chỉ là một loạt các chú thích cho Archimedes. Do đó, hóa ra Archimedes là nhà khoa học quan trọng nhất từng sống.

Archimedes là lý tưởng của tôi. Tôi ngưỡng mộ các tác phẩm của các nghệ sĩ, nhưng theo tôi, chúng chỉ là bóng tối và hình ảnh. Nhà phát minh, tôi nghĩ, mang đến cho thế giới những sáng tạo hữu hình, sống động và hoạt động.

5.2. Lễ kỷ niệm và Tưởng niệm

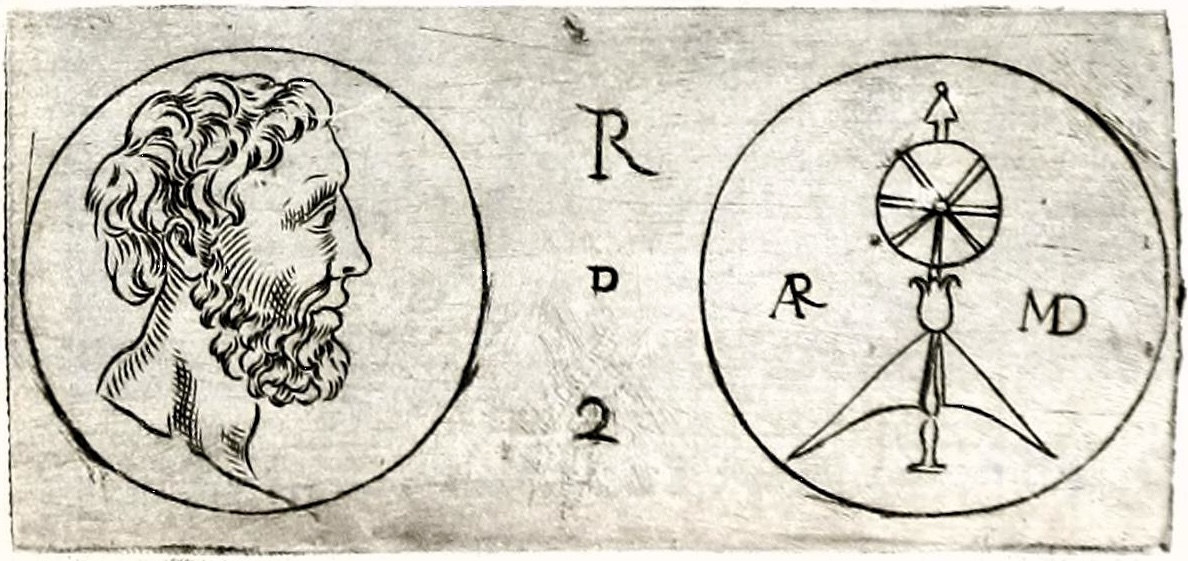
Nhà nghiên cứu tiền xu và khảo cổ học người Ý Filippo Paruta (1552-1629) và Leonardo Agostini (1593-1676) đã báo cáo về một đồng xu đồng ở Sicilia với chân dung Archimedes ở mặt trước và một hình trụ và hình cầu với chữ lồng ARMD bằng tiếng Latin ở mặt sau. Mặc dù đồng xu hiện đã mất và ngày đúc của nó không được biết chính xác, Ivo Schneider mô tả mặt sau là "một hình cầu nằm trên một đế - có lẽ là một hình ảnh thô sơ của một trong những cung thiên văn do Archimedes tạo ra," và gợi ý rằng nó có thể đã được đúc ở La Mã cho Marcellus, người "theo các báo cáo cổ đại, đã mang hai quả cầu của Archimedes về La Mã."

Có một miệng núi lửa trên Mặt Trăng tên là Archimedes (29.7° N, 4.0° W) để vinh danh ông, cũng như một dãy núi trên Mặt Trăng, Montes Archimedes (25.3° N, 4.6° W).

Huy chương Fields cho thành tựu xuất sắc trong toán học mang chân dung Archimedes, cùng với một hình khắc minh họa chứng minh của ông về hình cầu và hình trụ. Dòng chữ khắc quanh đầu Archimedes là một câu trích dẫn được gán cho nhà thơ thế kỷ 1 SCN Manilius, viết bằng tiếng Latin: Transire suum pectus mundoque potiri ("Vượt lên chính mình và nắm giữ thế giới").

Archimedes đã xuất hiện trên tem bưu chính do Đông Đức (1973), Hy Lạp (1983), Ý (1983), Nicaragua (1971), San Marino (1982), và Tây Ban Nha (1963) phát hành.

Lời kêu gọi "Eureka!" được gán cho Archimedes là khẩu hiệu của bang California. Trong trường hợp này, từ này ám chỉ việc khám phá vàng gần Sutter's Mill vào năm 1848, châm ngòi cho Cơn sốt vàng California.