1. Cuộc đời
Cuộc đời của Johann Carl Friedrich Gauss được đánh dấu bằng sự bộc lộ thiên tài từ sớm, những đóng góp học thuật đột phá trong nhiều lĩnh vực, và một đời sống cá nhân đầy thăng trầm.
1.1. Tuổi thơ và giáo dục


Johann Carl Friedrich Gauss sinh ngày 30 tháng 4 năm 1777 tại Braunschweig, thuộc Công quốc Braunschweig-Wolfenbüttel (nay là Niedersachsen, Đức). Gia đình ông có địa vị xã hội tương đối thấp. Cha ông, Gebhard Dietrich Gauss (1744-1808), làm nhiều nghề khác nhau như thợ làm thịt, thợ xây, người làm vườn và thủ quỹ của một quỹ trợ cấp tử tuất. Gauss mô tả cha mình là người đáng kính và được tôn trọng, nhưng cục cằn và gia trưởng ở nhà. Ông có kinh nghiệm trong việc viết và tính toán, trong khi người vợ thứ hai của ông, Dorothea, mẹ của Carl Friedrich, gần như mù chữ. Ông có một người anh trai cùng cha khác mẹ từ cuộc hôn nhân đầu tiên của cha mình.
Gauss là một thần đồng về toán học. Khi các giáo viên tiểu học nhận thấy khả năng trí tuệ của ông, họ đã báo cáo với Công tước Braunschweig, người đã gửi ông đến trường Collegium Carolinum địa phương, nơi ông theo học từ năm 1792 đến 1795, với Eberhard August Wilhelm von Zimmermann là một trong những giáo viên của ông. Sau đó, Công tước đã cấp cho ông nguồn lực để học toán, khoa học và ngôn ngữ cổ điển tại Đại học Göttingen cho đến năm 1798. Giáo sư toán học của ông là Abraham Gotthelf Kästner, người mà Gauss gọi là "nhà toán học hàng đầu trong số các nhà thơ, và nhà thơ hàng đầu trong số các nhà toán học" vì những bài epigram của ông. Thiên văn học được giảng dạy bởi Karl Felix Seyffer, người mà Gauss vẫn giữ liên lạc sau khi tốt nghiệp; Olbers và Gauss đã chế giễu ông trong thư từ của họ. Mặt khác, ông đánh giá cao Georg Christoph Lichtenberg, giáo viên vật lý của ông, và Christian Gottlob Heyne, người mà Gauss rất thích tham dự các bài giảng về cổ điển. Các bạn học cùng thời của ông là Johann Friedrich Benzenberg, Farkas Bolyai và Heinrich Wilhelm Brandes.
Ông có lẽ là một sinh viên tự học toán học vì ông đã độc lập tái khám phá một số định lý. Ông đã giải quyết một vấn đề hình học đã làm đau đầu các nhà toán học từ thời Hy Lạp cổ đại khi ông xác định vào năm 1796 những đa giác đều nào có thể được dựng bằng compa và thước kẻ. Khám phá này cuối cùng đã khiến Gauss chọn toán học thay vì bác ngữ học làm sự nghiệp. Nhật ký toán học của Gauss, một bộ sưu tập các ghi chú ngắn về kết quả của ông từ năm 1796 đến năm 1814, cho thấy nhiều ý tưởng cho tác phẩm toán học vĩ đại của ông, Disquisitiones Arithmeticae (1801), có từ thời điểm này.
1.2. Giai đoạn học giả tư nhân
Gauss tốt nghiệp Tiến sĩ Triết học vào năm 1799, không phải ở Göttingen như đôi khi được nói, mà theo yêu cầu đặc biệt của Công tước Braunschweig từ Đại học Helmstedt, trường đại học nhà nước duy nhất của công quốc. Johann Friedrich Pfaff đã đánh giá luận án tiến sĩ của ông, và Gauss nhận bằng in absentia mà không cần thi vấn đáp thêm. Công tước sau đó đã cấp cho ông chi phí sinh hoạt như một học giả tư nhân ở Brunswick. Gauss sau đó đã từ chối lời mời từ Viện Hàn lâm Khoa học Nga ở St. Peterburg và Đại học Landshut (nay là Đại học Ludwig Maximilian München). Sau đó, Công tước hứa sẽ thành lập một đài thiên văn ở Brunswick vào năm 1804. Kiến trúc sư Peter Joseph Krahe đã lập các bản thiết kế sơ bộ, nhưng một trong những cuộc chiến tranh của Napoléon đã hủy bỏ các kế hoạch đó: Công tước bị giết trong Trận Jena-Auerstedt năm 1806. Công quốc bị bãi bỏ vào năm sau, và sự hỗ trợ tài chính của Gauss chấm dứt.
Khi Gauss tính toán quỹ đạo tiểu hành tinh trong những năm đầu thế kỷ, ông đã thiết lập liên lạc với cộng đồng thiên văn học ở Bremen và Lilienthal, đặc biệt là Wilhelm Olbers, Karl Ludwig Harding và Friedrich Wilhelm Bessel, như một phần của nhóm thiên văn học không chính thức được gọi là Cảnh sát Thiên thể. Một trong những mục tiêu của họ là khám phá thêm các hành tinh. Họ thu thập dữ liệu về tiểu hành tinh và sao chổi làm cơ sở cho nghiên cứu của Gauss về quỹ đạo của chúng, mà ông sau này đã công bố trong tác phẩm thiên văn học vĩ đại của mình, Theoria motus corporum coelestium (1809).
1.3. Giai đoạn giáo sư tại Göttingen


Vào tháng 11 năm 1807, Gauss đã nhận lời mời đến Đại học Göttingen, lúc đó là một tổ chức của Vương quốc Westphalia mới thành lập dưới thời Jérôme Bonaparte, với tư cách là giáo sư chính thức và giám đốc đài thiên văn, và giữ chức vụ này cho đến khi ông qua đời vào năm 1855. Ông sớm phải đối mặt với yêu cầu nộp 2.000 franc từ chính phủ Westphalia như một khoản đóng góp chiến tranh, mà ông không thể chi trả. Cả Olbers và Laplace đều muốn giúp ông thanh toán, nhưng Gauss từ chối sự giúp đỡ của họ. Cuối cùng, một người ẩn danh từ Frankfurt, sau này được phát hiện là Thân vương-Tổng giám mục Dalberg, đã trả số tiền đó.
Gauss tiếp quản quyền giám đốc của đài thiên văn 60 năm tuổi, được thành lập vào năm 1748 bởi Tuyển hầu tước George II và được xây dựng trên một tháp pháo đài đã chuyển đổi, với các dụng cụ có thể sử dụng được, nhưng một phần đã lỗi thời. Việc xây dựng một đài thiên văn mới đã được Tuyển hầu tước George III chấp thuận về nguyên tắc từ năm 1802, và chính phủ Westphalia tiếp tục việc lập kế hoạch, nhưng Gauss không thể chuyển đến nơi làm việc mới của mình cho đến tháng 9 năm 1816. Ông có các dụng cụ mới hiện đại, bao gồm hai vòng kinh tuyến từ Repsold và Reichenbach, và một heliometer từ Fraunhofer.
Hoạt động khoa học của Gauss, ngoài toán học thuần túy, có thể được chia đại khái thành ba giai đoạn: thiên văn học là trọng tâm chính trong hai thập kỷ đầu của thế kỷ 19, trắc địa trong thập kỷ thứ ba, và vật lý, chủ yếu là từ học, trong thập kỷ thứ tư.
Gauss không giấu giếm sự ác cảm của mình đối với việc giảng bài học thuật. Nhưng từ khi bắt đầu sự nghiệp học thuật tại Göttingen, ông liên tục giảng bài cho đến năm 1854. Ông thường phàn nàn về gánh nặng giảng dạy, cảm thấy rằng đó là sự lãng phí thời gian của mình. Mặt khác, đôi khi ông mô tả một số sinh viên là tài năng. Hầu hết các bài giảng của ông đều liên quan đến thiên văn học, trắc địa và toán học ứng dụng, và chỉ ba bài giảng về các môn toán học thuần túy. Một số học trò của Gauss sau này đã trở thành những nhà toán học, vật lý học và thiên văn học nổi tiếng: Moritz Cantor, Dedekind, Dirksen, Encke, Gould, Heine, Klinkerfues, Kupffer, Listing, Möbius, Nicolai, Riemann, Ritter, Schering, Scherk, Schumacher, von Staudt, Stern, Ursin; cũng như các nhà khoa học địa chất Sartorius von Waltershausen và Wappäus.
Gauss không viết bất kỳ sách giáo khoa nào và không thích việc phổ biến khoa học. Những nỗ lực duy nhất của ông trong việc phổ biến là các công trình về ngày lễ Phục sinh (1800/1802) và bài tiểu luận Erdmagnetismus und Magnetometer năm 1836. Gauss chỉ xuất bản các bài báo và sách của mình bằng tiếng Latin hoặc tiếng Đức. Ông viết tiếng Latin theo phong cách cổ điển nhưng sử dụng một số sửa đổi thông thường do các nhà toán học đương thời đặt ra.
Trong bài giảng nhậm chức tại Đại học Göttingen năm 1808, Gauss tuyên bố rằng các quan sát đáng tin cậy và kết quả đạt được chỉ bằng một phép tính mạnh mẽ là những nhiệm vụ duy nhất của thiên văn học. Tại trường đại học, ông được đi cùng với đội ngũ giảng viên khác trong các lĩnh vực của mình, những người đã hoàn thành chương trình giáo dục; bao gồm nhà toán học Thibaut với các bài giảng của ông, nhà vật lý Mayer, người nổi tiếng với các sách giáo khoa của mình, người kế nhiệm ông Weber từ năm 1831, và tại đài thiên văn Harding, người đảm nhiệm phần lớn các bài giảng về thiên văn học thực hành. Khi đài thiên văn hoàn thành, Gauss chuyển đến chỗ ở mới ở cánh phía tây của đài thiên văn mới và Harding ở cánh phía đông. Họ từng là bạn bè thân thiết, nhưng theo thời gian họ trở nên xa cách, có thể - như một số nhà viết tiểu sử cho rằng - vì Gauss muốn Harding, người có cùng cấp bậc, chỉ là trợ lý hoặc quan sát viên của mình. Gauss gần như chỉ sử dụng các vòng kinh tuyến mới, và giữ chúng tránh xa Harding, ngoại trừ một số lần quan sát chung rất hiếm hoi.
Brendel chia hoạt động thiên văn của Gauss theo thời gian thành bảy giai đoạn, trong đó những năm từ 1820 được coi là "giai đoạn hoạt động thiên văn thấp hơn". Đài thiên văn mới, được trang bị tốt, không hoạt động hiệu quả như những đài khác; nghiên cứu thiên văn của Gauss có tính chất của một công việc cá nhân mà không có chương trình quan sát dài hạn, và trường đại học chỉ thiết lập một vị trí cho một trợ lý sau khi Harding qua đời vào năm 1834.
Tuy nhiên, Gauss hai lần từ chối cơ hội giải quyết vấn đề bằng cách chấp nhận lời đề nghị từ Berlin vào năm 1810 và 1825 để trở thành thành viên chính thức của Viện Hàn lâm Khoa học Phổ mà không phải chịu gánh nặng giảng dạy, cũng như từ Đại học Leipzig vào năm 1810 và từ Đại học Viên vào năm 1842, có lẽ vì tình hình gia đình khó khăn. Lương của Gauss được tăng từ 1.000 Reichsthaler vào năm 1810 lên 2.400 Reichsthaler vào năm 1824, và trong những năm cuối đời ông là một trong những giáo sư được trả lương cao nhất của trường đại học.
Khi Gauss được đồng nghiệp và bạn thân Friedrich Wilhelm Bessel nhờ giúp đỡ vào năm 1810, người đang gặp rắc rối tại Đại học Königsberg vì thiếu bằng cấp học thuật, Gauss đã cấp bằng tiến sĩ danh dự cho Bessel từ Khoa Triết học của Göttingen vào tháng 3 năm 1811. Gauss cũng đưa ra một khuyến nghị khác cho bằng cấp danh dự cho Sophie Germain nhưng chỉ ngay trước khi bà qua đời, vì vậy bà không bao giờ nhận được nó. Ông cũng hỗ trợ thành công nhà toán học Gotthold Eisenstein ở Berlin.
Gauss trung thành với Nhà Hannover. Sau khi Vua William IV qua đời vào năm 1837, Vua Hannover mới Ernest Augustus đã hủy bỏ hiến pháp năm 1833. Bảy giáo sư, sau này được gọi là "Göttingen Seven", đã phản đối điều này, trong số đó có bạn và cộng sự của ông là Wilhelm Weber và con rể của Gauss là Heinrich Ewald. Tất cả họ đều bị sa thải, và ba người trong số họ bị trục xuất, nhưng Ewald và Weber có thể ở lại Göttingen. Gauss bị ảnh hưởng sâu sắc bởi cuộc tranh cãi này nhưng không thấy khả năng giúp đỡ họ.
Gauss tham gia vào công việc quản lý học thuật: ba lần ông được bầu làm trưởng khoa Triết học. Được giao phụ trách quỹ lương hưu của góa phụ của trường đại học, ông đã nghiên cứu khoa học bảo hiểm và viết một báo cáo về chiến lược ổn định các khoản trợ cấp. Ông được bổ nhiệm làm giám đốc Viện Hàn lâm Khoa học Göttingen trong chín năm.
1.4. Đời sống gia đình
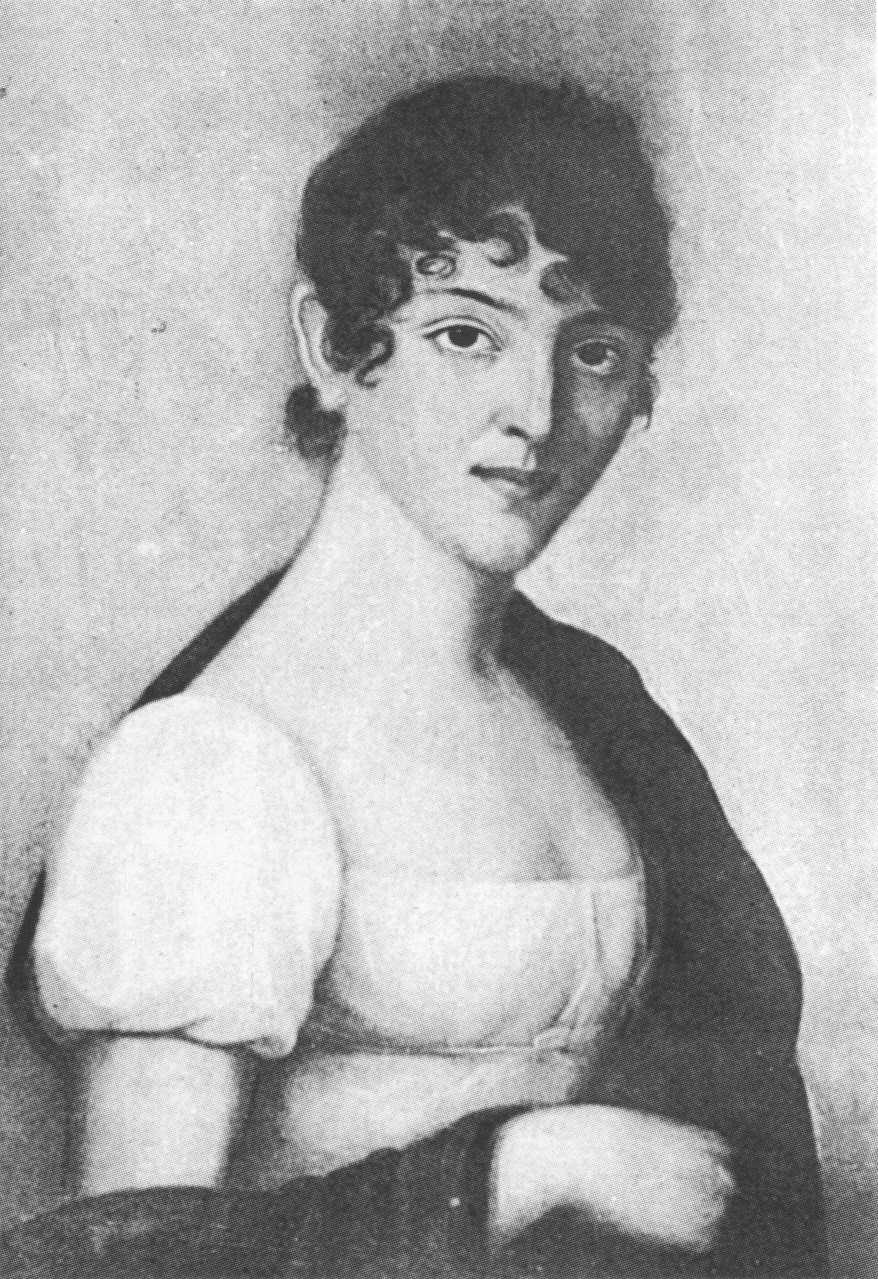
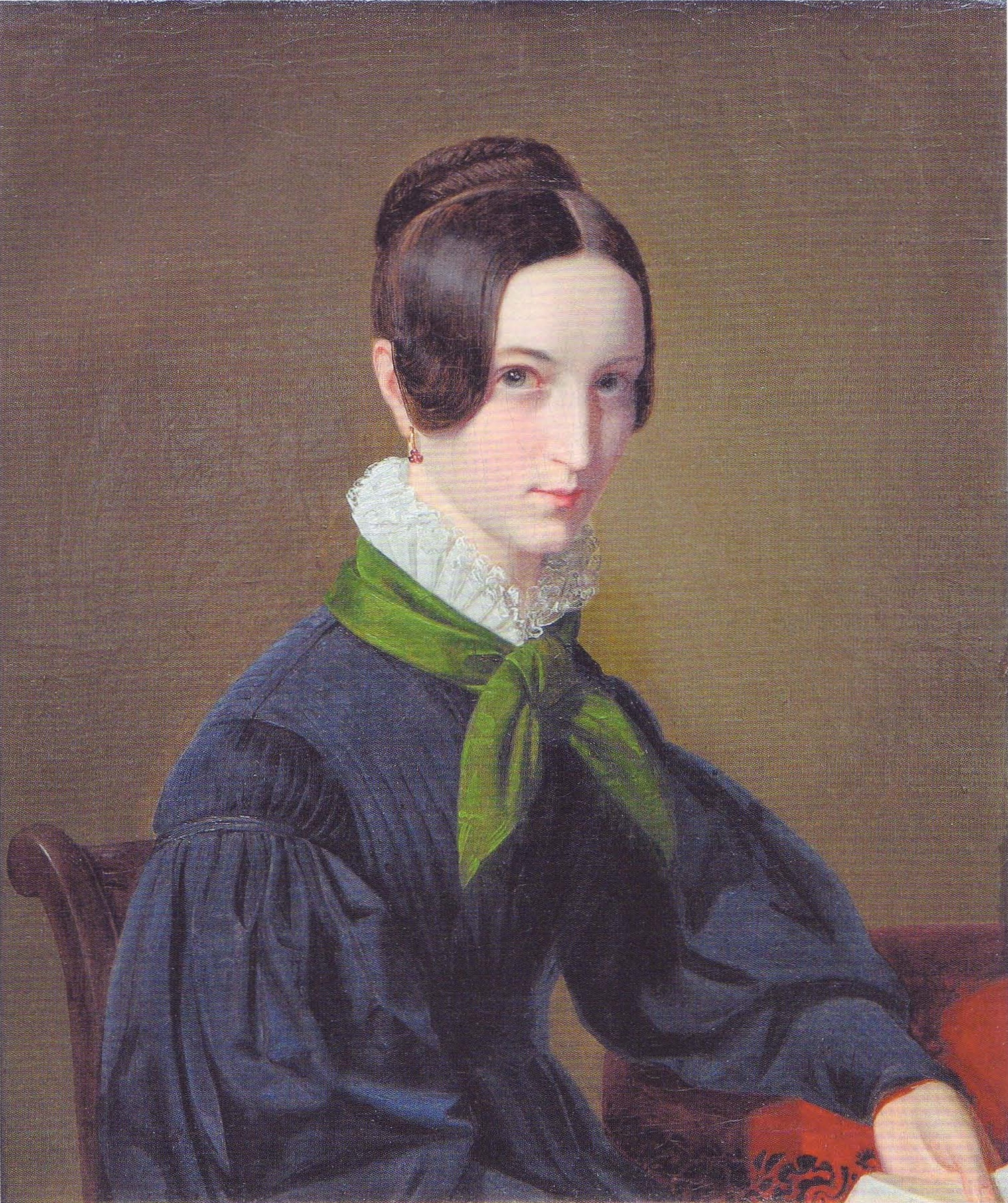
Gauss kết hôn với Johanna Osthoff vào ngày 9 tháng 10 năm 1805 tại nhà thờ St. Catherine ở Brunswick. Họ có hai con trai và một con gái: Joseph (1806-1873), Wilhelmina (1808-1840) và Louis (1809-1810). Johanna qua đời vào ngày 11 tháng 10 năm 1809, một tháng sau khi Louis ra đời, bản thân Louis cũng qua đời vài tháng sau đó. Gauss đã chọn tên của các con mình để vinh danh Giuseppe Piazzi, Wilhelm Olbers và Karl Ludwig Harding, những người khám phá ra các tiểu hành tinh đầu tiên.
Vào ngày 4 tháng 8 năm 1810, Gauss kết hôn với Wilhelmine (Minna) Waldeck, một người bạn của người vợ đầu tiên của ông, người mà ông có thêm ba người con: Eugen (sau này là Eugene) (1811-1896), Wilhelm (sau này là William) (1813-1879) và Therese (1816-1864). Minna Gauss qua đời vào ngày 12 tháng 9 năm 1831 sau khi bị bệnh nặng hơn một thập kỷ. Therese sau đó đã đảm nhận việc nhà và chăm sóc Gauss trong suốt quãng đời còn lại của ông; sau khi cha cô qua đời, cô kết hôn với diễn viên Constantin Staufenau. Chị gái cô là Wilhelmina kết hôn với nhà Đông phương học Heinrich Ewald. Mẹ của Gauss là Dorothea sống trong nhà ông từ năm 1817 cho đến khi bà qua đời vào năm 1839.
Con trai cả Joseph, khi còn là học sinh, đã giúp cha mình với tư cách là trợ lý trong chiến dịch khảo sát vào mùa hè năm 1821. Sau một thời gian ngắn học đại học, vào năm 1824 Joseph gia nhập Lục quân Hannover và hỗ trợ khảo sát trở lại vào năm 1829. Vào những năm 1830, ông chịu trách nhiệm mở rộng mạng lưới khảo sát đến các vùng phía tây của vương quốc. Với trình độ trắc địa của mình, ông rời quân ngũ và tham gia xây dựng mạng lưới đường sắt với tư cách là giám đốc Đường sắt Quốc gia Hannover. Năm 1836, ông đã nghiên cứu hệ thống đường sắt ở Mỹ trong vài tháng, nơi ông gặp nhà trắc địa Ferdinand Rudolph Hassler, người đã trao đổi thư từ khoa học với Carl Friedrich Gauss.
Eugen rời Göttingen vào tháng 9 năm 1830 và di cư sang Hoa Kỳ, nơi ông gia nhập quân đội trong năm năm. Sau đó ông làm việc cho American Fur Company ở Trung Tây Hoa Kỳ. Sau đó, ông chuyển đến Missouri và trở thành một doanh nhân thành đạt. Wilhelm kết hôn với một cháu gái của nhà thiên văn học Friedrich Bessel; ông sau đó chuyển đến Missouri, bắt đầu làm nông dân và trở nên giàu có trong ngành kinh doanh giày ở St. Louis trong những năm sau này. Eugene và William có rất nhiều hậu duệ ở Mỹ, nhưng tất cả hậu duệ của Gauss còn lại ở Đức đều xuất phát từ Joseph, vì các con gái không có con.







1.5. Tính cách và niềm tin
1.5.1. Học giả


Trong hai thập kỷ đầu của thế kỷ 19, Gauss là nhà toán học quan trọng duy nhất ở Đức, có thể so sánh với những nhà toán học hàng đầu của Pháp; Disquisitiones Arithmeticae của ông là cuốn sách toán học đầu tiên từ Đức được dịch sang tiếng Pháp.
Gauss "đi trước sự phát triển mới" với các nghiên cứu được ghi nhận từ năm 1799, sự phong phú của các ý tưởng mới và sự chặt chẽ trong chứng minh của ông. Trong khi các nhà toán học trước đây như Leonhard Euler cho phép độc giả tham gia vào lý luận của họ cho các ý tưởng mới, bao gồm cả những sai lệch nhất định khỏi con đường đúng đắn, Gauss lại giới thiệu một phong cách giải thích trực tiếp và hoàn chỉnh mới không cố gắng cho độc giả thấy quá trình tư duy của tác giả.
Ông đã khôi phục lại sự chặt chẽ trong chứng minh mà chúng ta ngưỡng mộ ở người xưa và đã bị đẩy lùi một cách không đáng có bởi sự quan tâm độc quyền của thời kỳ trước đối với những phát triển mới.
Nhưng đối với bản thân, ông lại truyền bá một lý tưởng hoàn toàn khác, được thể hiện trong một lá thư gửi Farkas Bolyai như sau:
Không phải là kiến thức, mà là hành động học hỏi, không phải sở hữu mà là hành động đạt được điều đó, mới mang lại niềm vui lớn nhất. Khi tôi đã làm rõ và khai thác cạn một chủ đề, thì tôi quay lưng lại với nó, để một lần nữa đi vào bóng tối.
Các bài báo được công bố sau khi ông qua đời, nhật ký khoa học của ông, và các ghi chú ngắn trong sách giáo khoa của riêng ông cho thấy ông đã làm việc theo kinh nghiệm ở một mức độ lớn. Ông là một nhà tính toán bận rộn và nhiệt tình suốt đời, người đã thực hiện các phép tính của mình với tốc độ phi thường, chủ yếu không cần kiểm soát chính xác, nhưng đã kiểm tra kết quả bằng cách ước tính thành thạo. Tuy nhiên, các phép tính của ông không phải lúc nào cũng không có lỗi. Ông đã đối phó với khối lượng công việc khổng lồ bằng cách sử dụng các công cụ khéo léo. Gauss đã sử dụng rất nhiều bảng toán học, kiểm tra độ chính xác của chúng và xây dựng các bảng mới về các vấn đề khác nhau để sử dụng cá nhân. Ông đã phát triển các công cụ mới để tính toán hiệu quả, ví dụ như phép khử Gauss. Người ta coi đó là một đặc điểm kỳ lạ trong phong cách làm việc của ông khi ông thực hiện các phép tính với độ chính xác cao hơn nhiều so với yêu cầu, và chuẩn bị các bảng với nhiều chữ số thập phân hơn mức cần thiết cho các mục đích thực tế. Rất có thể, phương pháp này đã cung cấp cho ông rất nhiều tài liệu mà ông đã sử dụng để tìm ra các định lý trong lý thuyết số.

Gauss từ chối xuất bản những công trình mà ông không cho là hoàn chỉnh và không thể bị chỉ trích. Sự hoàn hảo này phù hợp với phương châm trên con dấu cá nhân của ông: Pauca sed MaturaLatin ("Ít, nhưng chín chắn"). Nhiều đồng nghiệp đã khuyến khích ông công bố những ý tưởng mới và đôi khi khiển trách ông nếu ông chần chừ quá lâu, theo ý kiến của họ. Gauss tự bào chữa, cho rằng việc khám phá ban đầu các ý tưởng là dễ dàng, nhưng việc chuẩn bị một bản trình bày hoàn chỉnh là một vấn đề khó khăn đối với ông, do thiếu thời gian hoặc "sự thanh thản trong tâm trí". Tuy nhiên, ông đã công bố nhiều thông báo ngắn gọn về nội dung cấp bách trên nhiều tạp chí khác nhau, nhưng cũng để lại một di sản văn học đáng kể. Gauss gọi toán học là "nữ hoàng của các ngành khoa học" và số học là "nữ hoàng của toán học", và được cho là đã từng bày tỏ niềm tin vào sự cần thiết phải hiểu ngay lập tức đồng nhất thức Euler như một tiêu chuẩn để trở thành một nhà toán học hạng nhất.
Trong một số trường hợp, Gauss tuyên bố rằng những ý tưởng của một học giả khác đã từng thuộc sở hữu của ông trước đó. Do đó, khái niệm ưu tiên của ông là "người đầu tiên khám phá, không phải người đầu tiên công bố" khác với khái niệm của các nhà khoa học đương thời. Trái ngược với sự hoàn hảo của ông trong việc trình bày các ý tưởng toán học, ông bị chỉ trích vì cách trích dẫn cẩu thả. Ông tự bào chữa bằng một quan điểm rất đặc biệt về việc trích dẫn đúng: nếu ông đưa ra các tài liệu tham khảo, thì chỉ theo một cách khá đầy đủ, đối với các tác giả quan trọng trước đó, mà không ai nên bỏ qua; nhưng việc trích dẫn theo cách này cần kiến thức về lịch sử khoa học và nhiều thời gian hơn mức ông muốn dành.
1.5.2. Cá nhân
Ngay sau khi Gauss qua đời, người bạn Sartorius của ông đã xuất bản cuốn tiểu sử đầu tiên (1856), được viết theo một phong cách khá nhiệt tình. Sartorius nhìn ông như một người đàn ông điềm tĩnh và luôn tiến về phía trước với sự khiêm tốn như trẻ thơ, nhưng cũng có "tính cách sắt đá" với một sức mạnh tinh thần không thể lay chuyển. Ngoài vòng tròn thân thiết của ông, những người khác coi ông là người kín đáo và khó gần "như một Olympian ngồi ngự trị trên đỉnh cao khoa học". Những người đương thời gần gũi của ông đều đồng ý rằng Gauss là một người có tính cách khó khăn. Ông thường từ chối chấp nhận những lời khen ngợi. Khách của ông đôi khi khó chịu bởi thái độ gắt gỏng của ông, nhưng một thời gian ngắn sau đó tâm trạng của ông có thể thay đổi, và ông sẽ trở thành một chủ nhà quyến rũ, cởi mở. Gauss ghét những người có tính cách thích tranh cãi; cùng với đồng nghiệp Hausmann, ông đã phản đối việc mời Justus Liebig vào một ghế giáo sư đại học ở Göttingen, "vì ông ấy luôn dính líu đến một số cuộc tranh cãi."

Cuộc đời của Gauss bị che phủ bởi những vấn đề nghiêm trọng trong gia đình. Khi người vợ đầu Johanna đột ngột qua đời ngay sau khi sinh đứa con thứ ba, ông đã bộc lộ nỗi đau buồn trong một lá thư cuối cùng gửi người vợ đã mất theo phong cách của một threnody cổ đại, tài liệu cá nhân nhất còn sót lại của Gauss. Tình hình trở nên tồi tệ hơn khi bệnh lao cuối cùng đã hủy hoại sức khỏe của người vợ thứ hai Minna trong hơn 13 năm; cả hai con gái của ông sau này đều mắc cùng căn bệnh. Bản thân Gauss chỉ đưa ra những gợi ý nhỏ về nỗi đau khổ của mình: trong một lá thư gửi Bessel đề ngày tháng 12 năm 1831, ông tự mô tả mình là "nạn nhân của những đau khổ gia đình tồi tệ nhất".
Vì bệnh tật của vợ, cả hai con trai nhỏ đều được giáo dục trong vài năm ở Celle, xa Göttingen. Sự nghiệp quân sự của con trai cả Joseph kết thúc sau hơn hai thập kỷ với cấp bậc thiếu úy lương thấp, mặc dù ông đã có kiến thức đáng kể về trắc địa. Ông cần sự hỗ trợ tài chính từ cha mình ngay cả sau khi đã kết hôn. Con trai thứ hai Eugen thừa hưởng một phần lớn tài năng của cha mình về tính toán và ngôn ngữ nhưng có tính cách sôi nổi và đôi khi nổi loạn. Anh ấy muốn học bác ngữ học, trong khi Gauss muốn anh ấy trở thành một luật sư. Sau khi mắc nợ và gây ra một vụ bê bối công khai, Eugen đột ngột rời Göttingen trong hoàn cảnh kịch tính vào tháng 9 năm 1830 và di cư qua Bremen đến Hoa Kỳ. Anh ấy đã lãng phí số tiền ít ỏi mà anh ấy đã mang theo để bắt đầu, sau đó cha anh ấy từ chối hỗ trợ tài chính thêm. Con trai út Wilhelm muốn đủ điều kiện cho quản lý nông nghiệp, nhưng gặp khó khăn trong việc học tập phù hợp, và cuối cùng cũng di cư. Chỉ có con gái út Therese của Gauss đồng hành cùng ông trong những năm cuối đời.
Việc thu thập dữ liệu số về rất nhiều thứ khác nhau, hữu ích hay vô ích, đã trở thành một thói quen trong những năm cuối đời của ông, ví dụ, số lượng đường đi từ nhà ông đến một số địa điểm ở Göttingen, hoặc số ngày sống của các cá nhân; ông đã chúc mừng Humboldt vào tháng 12 năm 1851 vì đã đạt đến cùng tuổi với Isaac Newton khi ông qua đời, được tính bằng ngày.
Tương tự như kiến thức xuất sắc về tiếng Latin, ông cũng quen thuộc với các ngôn ngữ hiện đại. Ở tuổi 62, ông bắt đầu tự học tiếng Nga, rất có thể để hiểu các bài viết khoa học từ Nga, trong số đó có những bài của Lobachevsky về hình học phi Euclide. Gauss đọc cả văn học cổ điển và hiện đại, và các tác phẩm tiếng Anh và tiếng Pháp bằng ngôn ngữ gốc. Tác giả tiếng Anh yêu thích của ông là Walter Scott, tác giả tiếng Đức yêu thích của ông là Jean Paul. Gauss thích hát và đi hòa nhạc. Ông là một người đọc báo bận rộn; trong những năm cuối đời, ông thường đến một salon báo chí học thuật của trường đại học vào mỗi buổi trưa. Gauss không quan tâm nhiều đến triết học, và chế giễu "sự chia rẽ lông tóc của cái gọi là siêu hình học", ý ông là những người ủng hộ trường phái Naturphilosophie đương thời.
Gauss có một "tính cách quý tộc và hoàn toàn bảo thủ", ít tôn trọng trí thông minh và đạo đức của con người, theo phương châm "mundus vult decipi" (Thế giới muốn bị lừa dối, vậy hãy để nó bị lừa dối). Ông không thích Napoleon và hệ thống của ông, và mọi loại bạo lực và cách mạng đều gây ra sự kinh hoàng cho ông. Do đó, ông lên án các phương pháp của Cách mạng năm 1848, mặc dù ông đồng ý với một số mục tiêu của họ, chẳng hạn như ý tưởng về một nước Đức thống nhất. Về hệ thống chính trị, ông đánh giá thấp hệ thống hiến pháp; ông chỉ trích các nghị sĩ thời đó vì thiếu kiến thức và mắc lỗi logic.
Một số nhà viết tiểu sử của Gauss đã suy đoán về niềm tin tôn giáo của ông. Đôi khi ông nói "Chúa tính toán" và "Tôi đã thành công - không phải do những nỗ lực khó khăn của tôi, mà nhờ ân sủng của Chúa." Gauss là một thành viên của Giáo hội Luther, giống như hầu hết dân số ở miền bắc nước Đức. Có vẻ như ông không tin tất cả các tín điều hoặc hiểu Kinh Thánh theo nghĩa đen. Sartorius đã đề cập đến khoan dung tôn giáo của Gauss, và đánh giá "khát khao chân lý không ngừng" và ý thức công lý của ông là do niềm tin tôn giáo thúc đẩy.
1.5.3. Bộ não của Gauss
Ngày sau khi Gauss qua đời, bộ não của ông đã được lấy ra, bảo quản và nghiên cứu bởi Rudolf Wagner, người đã phát hiện khối lượng của nó hơi cao hơn mức trung bình, ở mức 1.49 K g. Con trai của Wagner là Hermann, một nhà địa lý học, đã ước tính diện tích vỏ não là 219.588 mm2 trong luận án tiến sĩ của mình. Năm 2013, một nhà thần kinh học tại Viện Max Planck về Hóa lý sinh ở Göttingen đã phát hiện ra rằng bộ não của Gauss đã bị nhầm lẫn ngay sau những cuộc điều tra đầu tiên, do dán nhãn sai, với bộ não của bác sĩ Conrad Heinrich Fuchs, người đã qua đời ở Göttingen vài tháng sau Gauss. Một cuộc điều tra sâu hơn cho thấy không có bất thường đáng chú ý nào trong bộ não của cả hai người. Do đó, tất cả các cuộc điều tra về bộ não của Gauss cho đến năm 1998, ngoại trừ những cuộc điều tra đầu tiên của Rudolf và Hermann Wagner, thực sự đề cập đến bộ não của Fuchs.
1.6. Qua đời và di sản
Gauss vẫn hoạt động trí óc cho đến tuổi già, ngay cả khi ông phải chịu đựng bệnh gout và sự không hạnh phúc nói chung. Vào ngày 23 tháng 2 năm 1855, ông qua đời vì một cơn đau tim ở Göttingen; và được an táng tại Nghĩa trang Albani ở đó. Heinrich Ewald, con rể của Gauss, và Wolfgang Sartorius von Waltershausen, bạn thân và nhà viết tiểu sử của Gauss, đã đọc lời điếu văn tại tang lễ của ông.
Gauss là một nhà đầu tư thành công và tích lũy được khối tài sản đáng kể với cổ phiếu và chứng khoán, cuối cùng có giá trị hơn 150.000 Thaler; sau khi ông qua đời, khoảng 18.000 Thaler được tìm thấy giấu trong phòng ông.
2. Công trình khoa học
Carl Friedrich Gauss đã có những đóng góp đột phá trong nhiều lĩnh vực khoa học, đặc biệt là toán học, thiên văn học và vật lý, định hình nhiều ngành học hiện đại.
2.1. Toán học
Các thành tựu toán học của Gauss bao gồm những đóng góp mang tính bước ngoặt trong lý thuyết số, đại số, giải tích, giải tích số, hình học vi phân, hình học phi Euclide và tô pô.
2.1.1. Lý thuyết số

Trong lời tựa của Disquisitiones Arithmeticae, Gauss ghi ngày bắt đầu công việc của mình về lý thuyết số là năm 1795. Bằng cách nghiên cứu các tác phẩm của các nhà toán học trước đó như Fermat, Euler, Lagrange và Legendre, ông nhận ra rằng những học giả này đã tìm thấy nhiều điều mà ông đã tự mình khám phá. Disquisitiones Arithmeticae, được viết vào năm 1798 và xuất bản năm 1801, đã củng cố lý thuyết số như một môn học và bao gồm cả lý thuyết số sơ cấp và lý thuyết số đại số. Trong đó, ông giới thiệu ký hiệu triple bar (≡) cho quan hệ đồng dư và sử dụng nó để trình bày rõ ràng số học mô đun. Nó đề cập đến định lý phân tích thừa số nguyên tố duy nhất và căn nguyên thủy modulo n. Trong các phần chính, Gauss trình bày hai chứng minh đầu tiên của luật tương hỗ bậc hai và phát triển các lý thuyết về dạng bậc hai nhị phân và dạng bậc hai tam phân.
Disquisitiones bao gồm luật hợp thành Gauss cho các dạng bậc hai nhị phân, cũng như việc liệt kê số lượng biểu diễn của một số nguyên dưới dạng tổng của ba số chính phương. Là một hệ quả gần như trực tiếp của định lý ba số chính phương của Legendre, ông chứng minh trường hợp tam giác của định lý số đa giác Fermat cho n = 3. Từ một số kết quả giải tích về nhóm lớp lý tưởng mà Gauss đưa ra mà không có bằng chứng ở cuối phần thứ năm, có vẻ như Gauss đã biết công thức số lớp vào năm 1801.
Trong phần cuối cùng, Gauss đưa ra bằng chứng về tính dựng được của một thất thập giác đều (đa giác 17 cạnh) bằng thước kẻ và compa bằng cách quy bài toán hình học này về một bài toán đại số. Ông chỉ ra rằng một đa giác đều có thể dựng được nếu số cạnh của nó là lũy thừa của 2 hoặc tích của lũy thừa của 2 và bất kỳ số số nguyên tố Fermat phân biệt nào. Trong cùng phần đó, ông đưa ra một kết quả về số nghiệm của một số đa thức bậc ba với các hệ số trong trường hữu hạn, tương đương với việc đếm các điểm nguyên trên một đường cong elliptic. Một chương thứ tám chưa hoàn thành đã được tìm thấy trong số các tài liệu còn lại sau khi ông qua đời, bao gồm công việc được thực hiện trong những năm 1797-1799.
Một trong những kết quả đầu tiên của Gauss là giả thuyết được tìm thấy theo kinh nghiệm vào năm 1792 - sau này được gọi là định lý số nguyên tố - đưa ra ước tính về số lượng số nguyên tố bằng cách sử dụng hàm tích phân logarit.
Khi Olbers khuyến khích Gauss vào năm 1816 để cạnh tranh một giải thưởng từ Viện Hàn lâm Pháp về chứng minh định lý cuối cùng của Fermat (FLT), ông đã từ chối vì đánh giá thấp vấn đề này. Tuy nhiên, trong số các tác phẩm còn lại của ông, một bài báo ngắn không đề ngày đã được tìm thấy với các chứng minh của FLT cho các trường hợp n = 3 và n = 5. Trường hợp cụ thể của n = 3 đã được Leonhard Euler chứng minh sớm hơn nhiều, nhưng Gauss đã phát triển một chứng minh hợp lý hơn, sử dụng số nguyên Eisenstein; mặc dù tổng quát hơn, chứng minh này đơn giản hơn trong trường hợp số nguyên thực.
Gauss đã đóng góp vào việc giải quyết giả thuyết Kepler vào năm 1831 với bằng chứng rằng mật độ đóng gói lớn nhất của các hình cầu trong không gian ba chiều được đưa ra khi tâm của các hình cầu tạo thành một sắp xếp lập phương tâm mặt, khi ông xem xét một cuốn sách của Ludwig August Seeber về lý thuyết rút gọn các dạng bậc ba dương. Sau khi nhận thấy một số thiếu sót trong chứng minh của Seeber, ông đã đơn giản hóa nhiều lập luận của mình, chứng minh giả thuyết trung tâm và nhận xét rằng định lý này tương đương với giả thuyết Kepler cho các sắp xếp đều đặn.
Trong hai bài báo về thặng dư bậc bốn (1828, 1832), Gauss đã giới thiệu vành của số nguyên Gauss , chỉ ra rằng đó là một miền phân tích duy nhất. và tổng quát hóa một số khái niệm số học chính, chẳng hạn như định lý nhỏ Fermat và bổ đề Gauss. Mục tiêu chính của việc giới thiệu vành này là để xây dựng luật tương hỗ bậc bốn - như Gauss đã khám phá, các vành số nguyên phức là môi trường tự nhiên cho các luật tương hỗ bậc cao hơn.
Trong bài báo thứ hai, ông đã nêu ra luật tổng quát về tương hỗ bậc bốn và chứng minh một số trường hợp đặc biệt của nó. Trong một ấn phẩm trước đó từ năm 1818 chứa chứng minh thứ năm và thứ sáu của ông về tương hỗ bậc hai, ông tuyên bố rằng các kỹ thuật của các chứng minh này (tổng Gauss) có thể được áp dụng để chứng minh các luật tương hỗ bậc cao hơn.
2.1.2. Đại số
Trong luận án tiến sĩ năm 1799, Gauss đã chứng minh định lý cơ bản của đại số rằng mọi đa thức đơn biến không đổi với các hệ số phức đều có ít nhất một nghiệm phức. Các nhà toán học bao gồm Jean le Rond d'Alembert đã đưa ra các chứng minh sai trước ông, và luận án của Gauss chứa một lời phê bình về công trình của d'Alembert. Sau đó, ông đã đưa ra ba chứng minh khác, chứng minh cuối cùng vào năm 1849 được coi là hoàn toàn chặt chẽ. Những nỗ lực của ông đã làm rõ khái niệm số phức một cách đáng kể.
2.1.3. Giải tích
Một trong những khám phá đầu tiên của Gauss là khái niệm trung bình cộng-hình học (AGM) của hai số thực dương. Ông đã khám phá ra mối quan hệ của nó với tích phân elliptic trong những năm 1798-1799 thông qua biến đổi Landen, và một mục nhật ký đã ghi lại việc khám phá mối liên hệ của hằng số Gauss với hàm elliptic lemniscate, một kết quả mà Gauss tuyên bố rằng "chắc chắn sẽ mở ra một lĩnh vực giải tích hoàn toàn mới". Ông cũng đã có những bước đột phá ban đầu vào các vấn đề hình thức hơn về nền tảng của giải tích phức, và từ một lá thư gửi Bessel vào năm 1811, rõ ràng là ông đã biết "định lý cơ bản của giải tích phức" - định lý tích phân Cauchy - và hiểu khái niệm thặng dư phức khi tích phân quanh các cực.
Định lý số ngũ giác của Euler, cùng với các nghiên cứu khác về AGM và hàm lemniscate, đã dẫn ông đến nhiều kết quả về hàm theta Jacobi, mà đỉnh cao là việc khám phá vào năm 1808 đồng nhất thức tích ba Jacobi, bao gồm định lý của Euler như một trường hợp đặc biệt. Các công trình của ông cho thấy ông đã biết các phép biến đổi modular bậc 3, 5, 7 cho các hàm elliptic từ năm 1808.
Một số mảnh vỡ toán học trong Nachlass của ông chỉ ra rằng ông đã biết một phần của lý thuyết hiện đại về dạng modular. Trong công trình của ông về AGM hàm đa trị của hai số phức, ông đã khám phá ra một mối liên hệ sâu sắc giữa vô số giá trị của AGM với hai "giá trị đơn giản nhất" của nó. Trong các bài viết chưa được công bố của mình, ông đã nhận ra và phác thảo khái niệm chính về miền cơ bản cho nhóm modular. Một trong những bản phác thảo của Gauss thuộc loại này là một bản vẽ về tessellation của đĩa đơn vị bằng các tam giác hyperbolic "đều" với tất cả các góc bằng .
Một ví dụ về cái nhìn sâu sắc của Gauss trong lĩnh vực giải tích là nhận xét khó hiểu rằng các nguyên tắc chia vòng tròn bằng compa và thước kẻ cũng có thể được áp dụng cho việc chia đường cong lemniscate, điều này đã truyền cảm hứng cho định lý của Abel về chia lemniscate. Một ví dụ khác là ấn phẩm "Summatio quarundam serierum singularium" (1811) của ông về việc xác định dấu của tổng Gauss bậc hai, trong đó ông đã giải quyết vấn đề chính bằng cách giới thiệu q-analog của hệ số nhị thức và thao tác chúng bằng một số đồng nhất thức gốc dường như bắt nguồn từ công trình của ông về lý thuyết hàm elliptic; tuy nhiên, Gauss đã đưa ra lập luận của mình theo một cách hình thức không tiết lộ nguồn gốc của nó trong lý thuyết hàm elliptic, và chỉ có công trình sau này của các nhà toán học như Jacobi và Hermite mới làm lộ ra điểm mấu chốt trong lập luận của ông.
Trong "Disquisitiones generales circa series infinitam..." (1813), ông cung cấp cách xử lý có hệ thống đầu tiên về hàm siêu hình học tổng quát , và chỉ ra rằng nhiều hàm được biết đến vào thời điểm đó là các trường hợp đặc biệt của hàm siêu hình học. Công trình này là công trình đầu tiên có một cuộc điều tra chính xác về sự hội tụ của chuỗi vô hạn trong lịch sử toán học. Hơn nữa, nó đề cập đến các phân số liên tục vô hạn phát sinh dưới dạng tỷ lệ của các hàm siêu hình học mà hiện nay được gọi là phân số liên tục Gauss.
Năm 1823, Gauss đã giành giải thưởng của Hiệp hội Đan Mạch với một bài tiểu luận về ánh xạ bảo giác, trong đó chứa một số phát triển liên quan đến lĩnh vực giải tích phức. Gauss tuyên bố rằng các ánh xạ bảo toàn góc trong mặt phẳng phức phải là các hàm giải tích phức, và sử dụng phương trình Beltrami sau này để chứng minh sự tồn tại của tọa độ đẳng nhiệt trên các bề mặt giải tích. Bài tiểu luận kết thúc bằng các ví dụ về ánh xạ bảo giác vào một hình cầu và một elipxoit quay.
2.1.4. Giải tích số
Gauss thường suy luận các định lý một cách quy nạp từ dữ liệu số mà ông đã thu thập theo kinh nghiệm. Do đó, việc sử dụng các thuật toán hiệu quả để tạo điều kiện thuận lợi cho các phép tính là rất quan trọng đối với nghiên cứu của ông, và ông đã có nhiều đóng góp cho giải tích số, như phương pháp cầu phương Gauss được công bố vào năm 1816.
Trong một lá thư riêng gửi Gerling từ năm 1823, ông đã mô tả một giải pháp cho hệ phương trình tuyến tính 4x4 bằng cách sử dụng phương pháp Gauss-Seidel - một phương pháp lặp "gián tiếp" để giải các hệ tuyến tính, và khuyến nghị nó hơn phương pháp "khử trực tiếp" thông thường cho các hệ có hơn hai phương trình.
Gauss đã phát minh ra một thuật toán để tính toán cái mà ngày nay được gọi là biến đổi Fourier rời rác, khi tính toán quỹ đạo của Pallas và Juno vào năm 1805, 160 năm trước khi Cooley và Tukey tìm thấy thuật toán FFT Cooley-Tukey tương tự của họ. Ông đã phát triển nó như một phương pháp nội suy lượng giác, nhưng bài báo Theoria Interpolationis Methodo Nova Tractata chỉ được xuất bản sau khi ông qua đời vào năm 1876, trước đó là bài trình bày đầu tiên của Joseph Fourier về chủ đề này vào năm 1807.
2.1.5. Hình học vi phân
Cuộc khảo sát trắc địa của Hannover đã thúc đẩy sự quan tâm của Gauss đến hình học vi phân và tô pô, các lĩnh vực toán học liên quan đến đường cong và bề mặt. Điều này đã dẫn ông vào năm 1828 đến việc công bố một chuyên luận đánh dấu sự ra đời của hình học vi phân của bề mặt hiện đại, vì nó đã thoát khỏi các cách truyền thống xử lý bề mặt như các đồ thị Descartes của các hàm hai biến, và bắt đầu khám phá các bề mặt từ quan điểm "bên trong" của một thực thể hai chiều bị giới hạn di chuyển trên đó. Kết quả là, Định lý Egregium (định lý đáng chú ý), đã thiết lập một tính chất của khái niệm độ cong Gauss. Một cách không chính thức, định lý nói rằng độ cong của một bề mặt có thể được xác định hoàn toàn bằng cách đo góc và khoảng cách trên bề mặt, bất kể sự nhúng của bề mặt trong không gian ba chiều hoặc hai chiều.
Định lý Egregium dẫn đến sự trừu tượng hóa các bề mặt như các đa tạp mở rộng kép; nó làm rõ sự phân biệt giữa các tính chất nội tại của đa tạp (metric) và sự hiện thực hóa vật lý của nó trong không gian xung quanh. Một hệ quả là không thể có một phép biến đổi đẳng cự giữa các bề mặt có độ cong Gauss khác nhau. Điều này có nghĩa là trên thực tế, một hình cầu hoặc một elipxoit không thể được biến đổi thành một mặt phẳng mà không bị biến dạng, điều này gây ra một vấn đề cơ bản trong việc thiết kế các phép chiếu bản đồ cho các bản đồ địa lý. Một phần của bài tiểu luận này dành cho một nghiên cứu sâu sắc về các đường trắc địa. Đặc biệt, Gauss chứng minh định lý Gauss-Bonnet địa phương trên các tam giác trắc địa, và tổng quát hóa định lý Legendre về tam giác cầu thành các tam giác trắc địa trên các bề mặt tùy ý với độ cong liên tục; ông phát hiện ra rằng các góc của một tam giác trắc địa "đủ nhỏ" lệch khỏi các góc của một tam giác phẳng có cùng cạnh theo một cách chỉ phụ thuộc vào các giá trị độ cong bề mặt tại các đỉnh của tam giác, bất kể hành vi của bề mặt trong phần bên trong tam giác.
Chuyên luận của Gauss từ năm 1828 thiếu khái niệm độ cong trắc địa. Tuy nhiên, trong một bản thảo chưa được công bố trước đó, rất có thể được viết vào năm 1822-1825, ông đã giới thiệu thuật ngữ "độ cong cạnh" (tiếng Đức: "Seitenkrümmung") và chứng minh tính bất biến của nó dưới các phép biến đổi đẳng cự, một kết quả sau này được Ferdinand Minding thu được và công bố vào năm 1830. Bài báo này của Gauss chứa cốt lõi của bổ đề của ông về độ cong tổng thể, nhưng cũng là sự tổng quát hóa của nó, được Pierre Ossian Bonnet tìm thấy và chứng minh vào năm 1848 và được biết đến là định lý Gauss-Bonnet.
2.1.6. Hình học phi Euclid
Trong suốt cuộc đời của Gauss, một cuộc thảo luận sôi nổi về tiên đề song song trong hình học Euclide đã diễn ra. Nhiều nỗ lực đã được thực hiện để chứng minh nó trong khuôn khổ các tiên đề Euclide, trong khi một số nhà toán học thảo luận về khả năng của các hệ thống hình học không có nó. Gauss đã suy nghĩ về các cơ sở của hình học từ những năm 1790, nhưng vào những năm 1810, ông nhận ra rằng một hình học phi Euclide không có tiên đề song song có thể giải quyết vấn đề. Trong một lá thư gửi Franz Taurinus năm 1824, ông trình bày một phác thảo ngắn gọn dễ hiểu về cái mà ông gọi là "hình học phi Euclid", nhưng ông nghiêm cấm Taurinus sử dụng nó. Gauss được ghi nhận là người đầu tiên khám phá và nghiên cứu hình học phi Euclide, thậm chí còn đặt ra thuật ngữ này.
Các ấn phẩm đầu tiên về hình học phi Euclide trong lịch sử toán học được viết bởi Nikolai Lobachevsky vào năm 1829 và Janos Bolyai vào năm 1832. Trong những năm tiếp theo, Gauss đã viết những ý tưởng của mình về chủ đề này nhưng không công bố chúng, do đó tránh ảnh hưởng đến cuộc thảo luận khoa học đương thời. Gauss đã ca ngợi những ý tưởng của Janos Bolyai trong một lá thư gửi cha của ông và người bạn đại học Farkas Bolyai, tuyên bố rằng những ý tưởng này trùng khớp với những suy nghĩ của ông từ vài thập kỷ trước. Tuy nhiên, không hoàn toàn rõ ràng ông đã đi trước Lobachevsky và Bolyai đến mức nào, vì những nhận xét trong thư của ông chỉ mơ hồ và khó hiểu.
Sartorius đã đề cập đến công trình của Gauss về hình học phi Euclide lần đầu tiên vào năm 1856, nhưng chỉ có ấn bản các bài báo còn lại trong Tập VIII của Tuyển tập công trình (1900) mới cho thấy những ý tưởng của Gauss về vấn đề đó, vào thời điểm mà hình học phi Euclide vẫn còn là một chủ đề gây tranh cãi.
2.1.7. Tô pô
Gauss cũng là một người tiên phong sớm của tô pô hay Geometria Situs, như nó được gọi vào thời của ông. Chứng minh đầu tiên của định lý cơ bản của đại số vào năm 1799 chứa một lập luận về cơ bản là tô pô; năm mươi năm sau, ông tiếp tục phát triển lập luận tô pô trong chứng minh thứ tư của định lý này.

Một cuộc gặp gỡ khác với các khái niệm tô pô xảy ra với ông trong quá trình làm việc về thiên văn học vào năm 1804, khi ông xác định giới hạn của vùng trên thiên cầu nơi sao chổi và tiểu hành tinh có thể xuất hiện, và ông gọi đó là "Zodiacus". Ông phát hiện ra rằng nếu quỹ đạo của Trái Đất và sao chổi được liên kết, thì vì lý do tô pô, Zodiacus là toàn bộ hình cầu. Năm 1848, trong bối cảnh khám phá tiểu hành tinh 7 Iris, ông đã công bố một cuộc thảo luận định tính sâu hơn về Zodiacus.
Trong các lá thư của Gauss từ năm 1820-1830, ông đã suy nghĩ sâu sắc về các chủ đề có mối liên hệ chặt chẽ với Geometria Situs, và dần dần nhận thức được khó khăn về ngữ nghĩa trong lĩnh vực này. Các mảnh vỡ từ thời kỳ này cho thấy ông đã cố gắng phân loại "hình dạng đường đi", là các đường cong phẳng kín có số lượng giao điểm tự cắt ngang hữu hạn, có thể cũng là các phép chiếu phẳng của nút. Để làm được điều đó, ông đã nghĩ ra một sơ đồ ký hiệu, mã Gauss, mà theo một nghĩa nào đó đã nắm bắt được các đặc điểm của hình dạng đường đi.
Trong một mảnh vỡ từ năm 1833, Gauss đã định nghĩa số liên kết của hai đường cong trong không gian bằng một tích phân kép nhất định, và bằng cách đó đã cung cấp lần đầu tiên một công thức giải tích cho một hiện tượng tô pô. Trong cùng một ghi chú, ông than thở về sự tiến bộ ít ỏi trong Geometria Situs, và nhận xét rằng một trong những vấn đề trung tâm của nó sẽ là "đếm các sự đan xen của hai đường cong kín hoặc vô hạn". Sổ ghi chép của ông từ thời kỳ đó cho thấy ông cũng đang suy nghĩ về các đối tượng tô pô khác như lý thuyết bện và tangle.
Ảnh hưởng của Gauss trong những năm sau này đối với lĩnh vực tô pô đang nổi lên, mà ông đánh giá cao, là thông qua các nhận xét và giao tiếp bằng lời nói thỉnh thoảng với Mobius và Listing.
2.1.8. Các thành tựu toán học nhỏ khác
Gauss đã áp dụng khái niệm số phức để giải quyết các vấn đề nổi tiếng theo một cách mới, ngắn gọn. Ví dụ, trong một ghi chú ngắn từ năm 1836 về các khía cạnh hình học của các dạng bậc ba và ứng dụng của chúng vào tinh thể học, ông đã nêu ra định lý cơ bản của axonometry, cho biết cách biểu diễn một khối lập phương 3D trên mặt phẳng 2D với độ chính xác hoàn toàn, thông qua số phức. Ông đã mô tả các phép quay của hình cầu này như là hành động của một số biến đổi phân tuyến tính trên mặt phẳng phức mở rộng, và đưa ra một chứng minh cho định lý hình học rằng các đường cao của một tam giác luôn gặp nhau tại một trực tâm duy nhất.
Gauss đã quan tâm đến "Pentagramma mirificum" của John Napier - một ngũ giác cầu nhất định - trong vài thập kỷ; ông đã tiếp cận nó từ nhiều góc độ khác nhau, và dần dần có được sự hiểu biết đầy đủ về các khía cạnh hình học, đại số và giải tích của nó. Đặc biệt, vào năm 1843, ông đã nêu ra và chứng minh một số định lý liên kết các hàm elliptic, các ngũ giác cầu Napier và các ngũ giác Poncelet trong mặt phẳng.
Hơn nữa, ông đã đóng góp một giải pháp cho vấn đề xây dựng hình elip có diện tích lớn nhất bên trong một tứ giác cho trước, và khám phá một kết quả đáng ngạc nhiên về việc tính toán diện tích của các ngũ giác.
2.2. Thiên văn học
Các thành tựu của Gauss trong thiên văn học bao gồm việc phát hiện và tính toán quỹ đạo của Ceres, lý thuyết nhiễu loạn tiểu hành tinh, khảo sát trắc địa và phát minh máy heliothrop.

Vào ngày 1 tháng 1 năm 1801, nhà thiên văn học người Ý Giuseppe Piazzi đã phát hiện ra một thiên thể mới, cho rằng đó là hành tinh đã được tìm kiếm từ lâu giữa Sao Hỏa và Sao Mộc theo cái gọi là định luật Titius-Bode, và đặt tên nó là Ceres. Ông chỉ có thể theo dõi nó trong một thời gian ngắn cho đến khi nó biến mất sau ánh sáng chói của Mặt Trời. Các công cụ toán học thời đó không đủ để ngoại suy một vị trí từ vài dữ liệu để nó xuất hiện trở lại. Gauss đã giải quyết vấn đề và dự đoán một vị trí để có thể tái khám phá vào tháng 12 năm 1801. Điều này hóa ra chính xác trong vòng nửa độ khi Franz Xaver von Zach vào ngày 7 và 31 tháng 12 tại Gotha, và độc lập Heinrich Olbers vào ngày 1 và 2 tháng 1 ở Bremen, đã xác định vật thể gần vị trí dự đoán.
Phương pháp của Gauss dẫn đến một phương trình bậc tám, trong đó một nghiệm, quỹ đạo của Trái Đất, đã được biết. Nghiệm cần tìm sau đó được tách ra khỏi sáu nghiệm còn lại dựa trên các điều kiện vật lý. Trong công trình này, Gauss đã sử dụng các phương pháp xấp xỉ toàn diện mà ông đã tạo ra cho mục đích đó.
Việc phát hiện ra Ceres đã dẫn Gauss đến lý thuyết về chuyển động của các hành tinh nhỏ bị nhiễu loạn bởi các hành tinh lớn, cuối cùng được xuất bản vào năm 1809 dưới tên Theoria motus corporum coelestium in sectionibus conicis solem ambientum. Nó đã giới thiệu hằng số hấp dẫn Gauss.
Kể từ khi các tiểu hành tinh mới được phát hiện, Gauss đã bận tâm với các nhiễu loạn của các yếu tố quỹ đạo của chúng. Đầu tiên, ông đã kiểm tra Ceres bằng các phương pháp phân tích tương tự như của Laplace, nhưng đối tượng yêu thích của ông là Pallas, vì độ lệch tâm lớn và độ nghiêng quỹ đạo của nó, do đó phương pháp của Laplace không hoạt động. Gauss đã sử dụng các công cụ của riêng mình: trung bình cộng-hình học, hàm siêu hình học và phương pháp nội suy của ông. Ông đã tìm thấy một cộng hưởng quỹ đạo với Sao Mộc theo tỷ lệ 18:7 vào năm 1812; Gauss đã đưa ra kết quả này dưới dạng mật mã, và chỉ đưa ra ý nghĩa rõ ràng trong các lá thư gửi Olbers và Bessel. Sau nhiều năm làm việc, ông đã hoàn thành nó vào năm 1816 mà không có kết quả nào mà ông cho là đủ. Điều này đánh dấu sự kết thúc các hoạt động của ông trong thiên văn học lý thuyết.

Một kết quả của nghiên cứu của Gauss về nhiễu loạn Pallas là Determinatio Attractionis... (1818) về một phương pháp thiên văn học lý thuyết sau này được gọi là "phương pháp vòng elip". Nó giới thiệu một khái niệm trung bình hóa trong đó một hành tinh trên quỹ đạo được thay thế bằng một vòng giả định với mật độ khối lượng tỷ lệ với thời gian hành tinh đi theo các cung quỹ đạo tương ứng. Gauss trình bày phương pháp đánh giá lực hấp dẫn của một vòng elip như vậy, bao gồm một số bước; một trong số đó liên quan đến việc áp dụng trực tiếp thuật toán trung bình cộng-hình học (AGM) để tính toán một tích phân elliptic.
Trong khi những đóng góp của Gauss cho thiên văn học lý thuyết kết thúc, các hoạt động thực tiễn hơn trong thiên văn học quan sát vẫn tiếp tục và chiếm giữ ông trong suốt sự nghiệp của mình. Ngay từ đầu năm 1799, Gauss đã giải quyết vấn đề xác định kinh độ bằng cách sử dụng thị sai Mặt Trăng, mà ông đã phát triển các công thức thuận tiện hơn so với những công thức đang được sử dụng phổ biến. Sau khi được bổ nhiệm làm giám đốc đài thiên văn, ông đã chú trọng đến các hằng số thiên văn cơ bản trong thư từ với Bessel. Bản thân Gauss đã cung cấp các bảng cho tuế sai và quang sai, tọa độ Mặt Trời và khúc xạ. Ông đã có nhiều đóng góp cho hình học cầu, và trong bối cảnh này đã giải quyết một số vấn đề thực tế về hàng hải bằng sao. Ông đã công bố một số lượng lớn các quan sát, chủ yếu về các hành tinh nhỏ và sao chổi; quan sát cuối cùng của ông là nhật thực ngày 28 tháng 7 năm 1851.
2.3. Vật lý
Gauss đã có những khám phá và lý thuyết quan trọng trong nhiều lĩnh vực vật lý khác nhau như địa từ học, điện từ học, lý thuyết thế năng, quang học, cơ học và đo lường học.
2.3.1. Địa từ học


Gauss đã quan tâm đến từ học từ năm 1803. Sau khi Alexander von Humboldt đến thăm Göttingen vào năm 1826, cả hai nhà khoa học đã bắt đầu nghiên cứu chuyên sâu về địa từ học, một phần độc lập, một phần hợp tác hiệu quả. Năm 1828, Gauss là khách của Humboldt trong hội nghị của Hiệp hội các nhà khoa học tự nhiên và bác sĩ Đức ở Berlin, nơi ông làm quen với nhà vật lý Wilhelm Weber.
Khi Weber nhận ghế vật lý ở Göttingen với tư cách là người kế nhiệm Johann Tobias Mayer theo khuyến nghị của Gauss vào năm 1831, cả hai đã bắt đầu một sự hợp tác hiệu quả, dẫn đến kiến thức mới về từ học với một biểu diễn cho đơn vị từ học theo khối lượng, điện tích và thời gian. Họ đã thành lập Hiệp hội Từ học (tiếng Đức: Magnetischer Verein), một nhóm làm việc quốc tế gồm một số đài thiên văn, đã hỗ trợ các phép đo từ trường Trái Đất ở nhiều vùng trên thế giới bằng các phương pháp giống nhau vào các ngày đã định từ năm 1836 đến 1841.
Năm 1836, Humboldt đã đề xuất thành lập một mạng lưới các trạm địa từ học trên toàn thế giới trong các lãnh thổ thuộc Anh bằng một lá thư gửi Công tước Sussex, lúc đó là chủ tịch Hội Hoàng gia Luân Đôn; ông đề xuất rằng các phép đo từ trường nên được thực hiện trong các điều kiện tiêu chuẩn hóa bằng cách sử dụng các phương pháp của ông. Cùng với các nhà khởi xướng khác, điều này đã dẫn đến một chương trình toàn cầu được gọi là "chiến dịch từ học" dưới sự chỉ đạo của Edward Sabine. Ngày, giờ và khoảng thời gian quan sát được xác định trước, giờ trung bình Göttingen được sử dụng làm tiêu chuẩn. 61 trạm trên cả năm lục địa đã tham gia vào chương trình toàn cầu này. Gauss và Weber đã thành lập một loạt ấn phẩm để công bố kết quả, sáu tập đã được xuất bản từ năm 1837 đến 1843. Việc Weber rời đến Leipzig vào năm 1843 do hậu quả muộn của vụ Göttingen Seven đã đánh dấu sự kết thúc hoạt động của Hiệp hội Từ học.
Theo gương Humboldt, Gauss đã ra lệnh xây dựng một đài thiên văn từ học trong vườn của đài thiên văn, nhưng các nhà khoa học khác nhau về thiết bị; Gauss thích các dụng cụ cố định, mà ông nghĩ sẽ cho kết quả chính xác hơn, trong khi Humboldt quen với các dụng cụ di động. Gauss quan tâm đến sự biến đổi theo thời gian và không gian của độ lệch từ, độ nghiêng và cường độ, nhưng phân biệt khái niệm cường độ từ của Humboldt với các thuật ngữ cường độ "ngang" và "dọc". Cùng với Weber, ông đã phát triển các phương pháp đo các thành phần của cường độ từ trường và xây dựng một từ kế phù hợp để đo giá trị tuyệt đối của cường độ từ trường Trái Đất, không còn là những giá trị tương đối phụ thuộc vào thiết bị. Độ chính xác của từ kế cao hơn khoảng mười lần so với các dụng cụ trước đó. Với công trình này, Gauss là người đầu tiên suy ra một đại lượng phi cơ học bằng các đại lượng cơ học cơ bản.
Gauss đã thực hiện một Lý thuyết chung về từ trường Trái Đất (1839), trong đó ông tin rằng đã mô tả bản chất của lực từ; theo Felix Klein, công trình này là một trình bày các quan sát bằng cách sử dụng hàm điều hòa cầu hơn là một lý thuyết vật lý. Lý thuyết này dự đoán sự tồn tại của chính xác hai cực từ trên Trái Đất, do đó ý tưởng của Hansteen về bốn cực từ trở nên lỗi thời, và dữ liệu cho phép xác định vị trí của chúng với độ chính xác khá tốt.
Gauss đã ảnh hưởng đến sự khởi đầu của địa vật lý ở Nga, khi Adolph Theodor Kupffer, một trong những học trò cũ của ông, đã thành lập một đài thiên văn từ học ở St. Petersburg, theo gương đài thiên văn ở Göttingen, và tương tự, Ivan Simonov ở Kazan.
2.3.2. Điện từ học
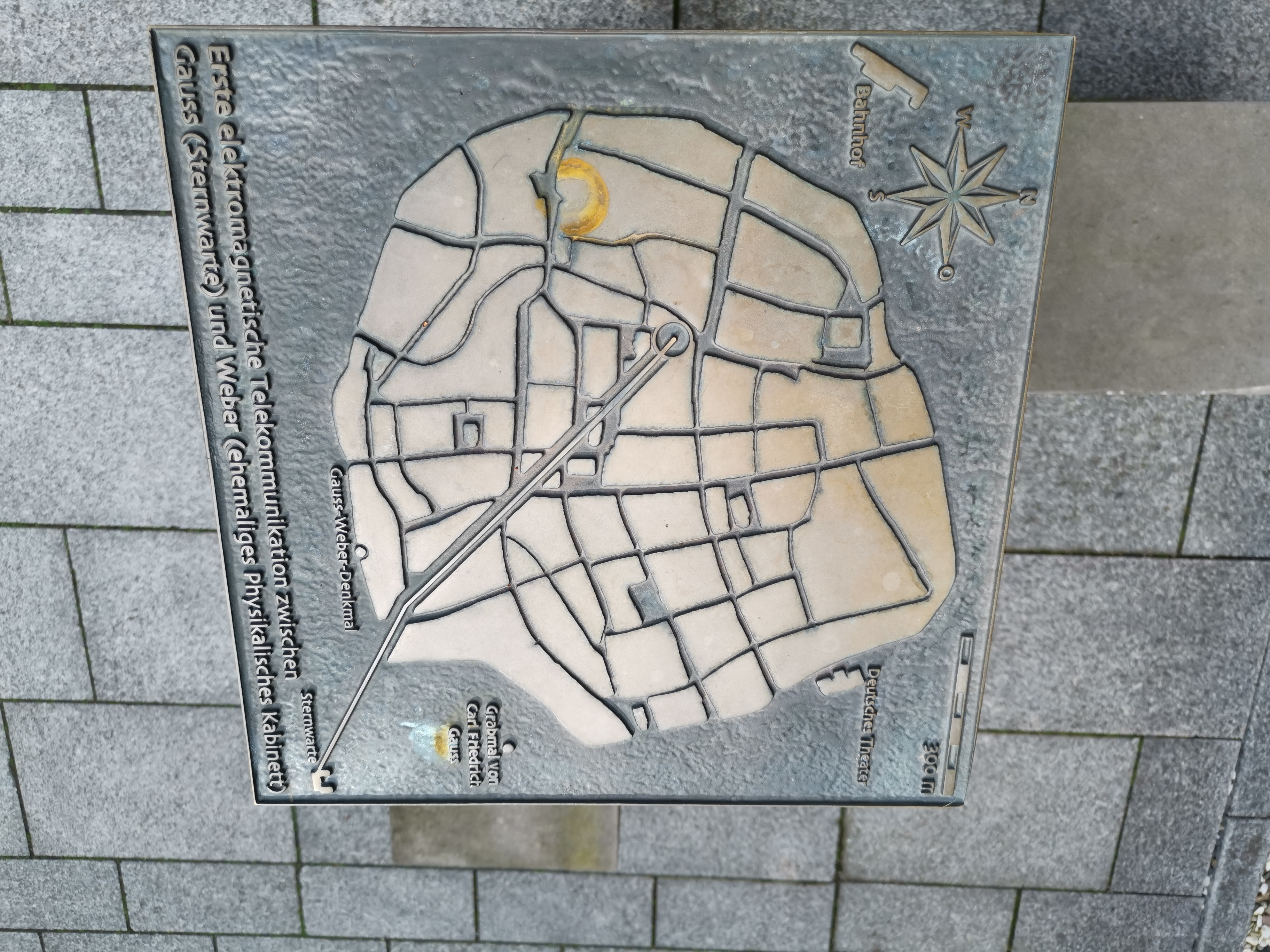
Các khám phá của Hans Christian Ørsted về điện từ học và Michael Faraday về cảm ứng điện từ đã thu hút sự chú ý của Gauss đến các vấn đề này. Gauss và Weber đã tìm ra các quy tắc cho các mạch điện phân nhánh, sau này được tìm thấy độc lập và lần đầu tiên được Gustav Kirchhoff công bố và đặt tên theo ông là định luật Kirchhoff về mạch điện, và đã thực hiện các cuộc điều tra về điện từ học. Họ đã xây dựng máy điện báo điện cơ đầu tiên vào năm 1833, và bản thân Weber đã kết nối đài thiên văn với viện vật lý ở trung tâm thị trấn Göttingen, nhưng họ không quan tâm đến bất kỳ sự phát triển nào nữa của phát minh này cho mục đích thương mại.
Các mối quan tâm lý thuyết chính của Gauss trong điện từ học được phản ánh trong những nỗ lực của ông nhằm xây dựng các định luật định lượng điều chỉnh cảm ứng điện từ. Trong các sổ ghi chép từ những năm này, ông đã ghi lại một số công thức sáng tạo; ông đã khám phá ra ý tưởng về hàm thế vector (được Franz Ernst Neumann độc lập tái khám phá vào năm 1845), và vào tháng 1 năm 1835, ông đã viết ra một "định luật cảm ứng" tương đương với định luật cảm ứng Faraday, trong đó nêu rõ rằng lực điện động tại một điểm nhất định trong không gian bằng với tốc độ thay đổi tức thời (theo thời gian) của hàm này.
Gauss đã cố gắng tìm một định luật thống nhất cho các hiệu ứng tầm xa của tĩnh điện, điện động lực học, điện từ học và cảm ứng điện, tương tự như định luật hấp dẫn của Newton, nhưng nỗ lực của ông đã kết thúc trong một "thất bại bi thảm".
2.3.3. Lý thuyết thế năng
Kể từ khi Isaac Newton đã chứng minh về mặt lý thuyết rằng Trái Đất và các ngôi sao quay có hình dạng không cầu, vấn đề hấp dẫn của các elipxoit đã trở nên quan trọng trong thiên văn học toán học. Trong ấn phẩm đầu tiên của ông về lý thuyết thế năng, "Theoria attractionis..." (1813), Gauss đã cung cấp một biểu thức dạng đóng cho lực hấp dẫn của một elipxoit ba trục đồng nhất tại mọi điểm trong không gian. Trái ngược với nghiên cứu trước đây của Maclaurin, Laplace và Lagrange, giải pháp mới của Gauss xử lý lực hấp dẫn trực tiếp hơn dưới dạng một tích phân elip. Trong quá trình đó, ông cũng chứng minh và áp dụng một số trường hợp đặc biệt của cái gọi là định lý Gauss trong giải tích vector.
Trong Các định lý chung liên quan đến các lực hấp dẫn và đẩy tác dụng theo tỷ lệ nghịch của khoảng cách bậc hai (1840), Gauss đã đưa ra nền tảng của một lý thuyết về thế từ vector, dựa trên Lagrange, Laplace và Poisson; có vẻ khá khó xảy ra là ông biết các công trình trước đó của George Green về chủ đề này. Tuy nhiên, Gauss không bao giờ có thể đưa ra bất kỳ lý do nào cho từ học, cũng như một lý thuyết về từ học tương tự như công trình của Newton về hấp dẫn, cho phép các nhà khoa học dự đoán các hiệu ứng địa từ trong tương lai.
2.3.4. Quang học
Các phép tính của Gauss đã giúp nhà chế tạo dụng cụ Johann Georg Repsold ở Hamburg chế tạo một hệ thống thấu kính sắc nét mới vào năm 1810. Một vấn đề chính, trong số các khó khăn khác, là kiến thức không chính xác về chiết suất và tán sắc của các loại kính được sử dụng. Trong một bài báo ngắn từ năm 1817, Gauss đã giải quyết vấn đề loại bỏ quang sai sắc trong thấu kính kép, và tính toán các điều chỉnh về hình dạng và hệ số khúc xạ cần thiết để giảm thiểu nó. Công trình của ông đã được nhà quang học Carl August von Steinheil ghi nhận, người vào năm 1860 đã giới thiệu thấu kính kép Steinheil sắc nét, một phần dựa trên các phép tính của Gauss. Nhiều kết quả trong quang học hình học chỉ rải rác trong các thư từ và ghi chú tay của Gauss.
Trong Nghiên cứu khúc xạ (1840), Gauss đã đưa ra phân tích có hệ thống đầu tiên về sự hình thành hình ảnh dưới phép tính xấp xỉ bàng trục (quang học Gauss). Ông đã mô tả các hệ thống quang học dưới phép tính xấp xỉ bàng trục chỉ bằng các điểm chính của nó, và ông đã suy ra công thức thấu kính Gauss, áp dụng không giới hạn đối với độ dày của thấu kính.
2.3.5. Cơ học
Công việc đầu tiên của Gauss trong cơ học liên quan đến sự tự quay của Trái Đất. Khi người bạn đại học của ông là Benzenberg thực hiện các thí nghiệm để xác định độ lệch của khối lượng rơi khỏi đường vuông góc vào năm 1802, điều mà ngày nay được biết đến là hiệu ứng của lực Coriolis, ông đã hỏi Gauss về một phép tính dựa trên lý thuyết về các giá trị để so sánh với các giá trị thực nghiệm. Gauss đã xây dựng một hệ thống các phương trình cơ bản cho chuyển động, và các kết quả tương ứng đủ với dữ liệu của Benzenberg, người đã thêm các cân nhắc của Gauss vào phụ lục cuốn sách của ông về các thí nghiệm rơi.
Sau khi Foucault đã chứng minh sự tự quay của Trái Đất bằng thí nghiệm con lắc Foucault của ông trước công chúng vào năm 1851, Gerling đã hỏi Gauss để giải thích thêm. Điều này đã thúc đẩy Gauss thiết kế một thiết bị mới để trình diễn với chiều dài con lắc ngắn hơn nhiều so với của Foucault. Các dao động được quan sát bằng một kính thiên văn đọc, với một thang đo dọc và một gương gắn vào con lắc. Nó được mô tả trong thư từ Gauss-Gerling và Weber đã thực hiện một số thí nghiệm với thiết bị này vào năm 1853, nhưng không có dữ liệu nào được công bố.
Nguyên lý ràng buộc tối thiểu của Gauss năm 1829 được thiết lập như một khái niệm chung để khắc phục sự phân chia cơ học thành tĩnh học và động lực học, kết hợp nguyên lý D'Alembert với nguyên lý công ảo của Lagrange, và cho thấy sự tương tự với phương pháp bình phương tối thiểu.
2.3.6. Đo lường học
Năm 1828, Gauss được bổ nhiệm làm trưởng ban Tiêu chuẩn cân đo của Vương quốc Hannover. Ông đã chỉ đạo việc tạo ra các tiêu chuẩn về chiều dài và các phép đo. Bản thân Gauss đã đảm nhiệm các phép đo tốn thời gian và đưa ra các chỉ dẫn chi tiết cho việc chuẩn bị cơ học. Trong thư từ với Schumacher, người cũng đang làm việc về vấn đề này, ông đã mô tả những ý tưởng mới cho các thang đo có độ chính xác cao. Ông đã đệ trình các báo cáo cuối cùng về foot và pound của Hannover lên chính phủ vào năm 1841. Công trình này có ý nghĩa hơn cả khu vực nhờ một luật năm 1836 đã liên kết các phép đo của Hannover với các phép đo của Anh.
2.4. Đo cung và khảo sát trắc địa



Gauss đã bận rộn với các vấn đề trắc địa từ năm 1799 khi ông giúp Karl Ludwig von Lecoq tính toán trong cuộc khảo sát của ông ở Westphalia. Bắt đầu từ năm 1804, ông tự học một số thực hành trắc địa với một kính lục phân ở Brunswick, và Göttingen.
Từ năm 1816, học trò cũ của Gauss là Heinrich Christian Schumacher, lúc đó là giáo sư ở Copenhagen, nhưng sống ở Altona (Công quốc Holstein) gần Hamburg với tư cách là người đứng đầu một đài thiên văn, đã thực hiện một phép đo tam giác của bán đảo Jutland từ Skagen ở phía bắc đến Lauenburg ở phía nam. Dự án này là cơ sở để sản xuất bản đồ nhưng cũng nhằm mục đích xác định cung trắc địa giữa các địa điểm cuối. Dữ liệu từ các cung trắc địa được sử dụng để xác định kích thước của geoid Trái Đất, và các khoảng cách cung dài mang lại kết quả chính xác hơn. Schumacher đã yêu cầu Gauss tiếp tục công việc này xa hơn về phía nam ở Vương quốc Hannover; Gauss đã đồng ý sau một thời gian ngắn do dự. Cuối cùng, vào tháng 5 năm 1820, Vua George IV đã ra lệnh cho Gauss.
Một đo cung cần xác định thiên văn chính xác ít nhất hai điểm trong mạng lưới. Gauss và Schumacher đã tận dụng cơ hội thuận lợi là cả hai đài thiên văn ở Göttingen và Altona, trong vườn nhà Schumacher, đều nằm gần như cùng một kinh độ. Vĩ độ được đo bằng cả hai dụng cụ của họ và một zenith sector của Ramsden đã được vận chuyển đến cả hai đài thiên văn.
Gauss và Schumacher đã xác định một số góc giữa Lüneburg, Hamburg và Lauenburg để kết nối trắc địa vào tháng 10 năm 1818. Trong các mùa hè từ 1821 đến 1825, Gauss đã trực tiếp chỉ đạo công việc tam giác hóa, từ Thuringia ở phía nam đến sông Elbe ở phía bắc. tam giác giữa Hoher Hagen, Großer Inselsberg trong Rừng Thuringia và Brocken trong dãy núi Harz là tam giác lớn nhất mà Gauss từng đo với kích thước tối đa là 107 km. Ở Lüneburg Heath dân cư thưa thớt mà không có đỉnh tự nhiên đáng kể hoặc các tòa nhà nhân tạo, ông đã gặp khó khăn trong việc tìm các điểm tam giác phù hợp; đôi khi cần phải cắt các làn đường xuyên qua thảm thực vật.
Để chỉ tín hiệu, Gauss đã phát minh ra một dụng cụ mới với gương di động và một kính thiên văn nhỏ phản chiếu tia nắng mặt trời đến các điểm tam giác, và đặt tên nó là heliotrope. Một cấu trúc phù hợp khác cho cùng mục đích là một kính lục phân với một gương bổ sung mà ông đặt tên là heliotrope phụ. Gauss đã nhận được sự hỗ trợ của binh lính quân đội Hannover, trong số đó có con trai cả Joseph của ông. Gauss đã tham gia vào phép đo đường cơ sở (Braak Base Line) của Schumacher ở làng Braak gần Hamburg vào năm 1820, và sử dụng kết quả để đánh giá phép tam giác hóa Hannover.
Một kết quả bổ sung là giá trị tốt hơn của độ dẹt của elipxoit Trái Đất gần đúng. Gauss đã phát triển phép chiếu Mercator ngang phổ quát của Trái Đất hình elip (mà ông gọi là phép chiếu đồng dạng) để biểu diễn dữ liệu trắc địa trong các biểu đồ phẳng.
Khi phép đo cung kết thúc, Gauss bắt đầu mở rộng phép tam giác hóa về phía tây để khảo sát toàn bộ Vương quốc Hannover theo sắc lệnh Hoàng gia ngày 25 tháng 3 năm 1828. Công việc thực tế được chỉ đạo bởi ba sĩ quan quân đội, trong số đó có Trung úy Joseph Gauss. Việc đánh giá dữ liệu hoàn chỉnh nằm trong tay Gauss, người đã áp dụng các phát minh toán học của mình như phương pháp bình phương tối thiểu và phép khử Gauss vào đó. Dự án kết thúc vào năm 1844, và Gauss đã gửi báo cáo cuối cùng của dự án cho chính phủ; phương pháp chiếu của ông không được chỉnh sửa cho đến năm 1866.
Năm 1828, khi nghiên cứu sự khác biệt về vĩ độ, Gauss lần đầu tiên định nghĩa một phép xấp xỉ vật lý cho hình dạng Trái Đất là bề mặt vuông góc với hướng trọng lực ở mọi nơi; sau này học trò tiến sĩ của ông là Johann Benedict Listing đã gọi đây là geoid.
3. Vinh danh và giải thưởng

Tư cách thành viên đầu tiên của một hội khoa học được trao cho Gauss vào năm 1802 bởi Viện Hàn lâm Khoa học Nga. Các tư cách thành viên khác (tương ứng, nước ngoài hoặc đầy đủ) được trao từ Viện Hàn lâm Khoa học Göttingen (1802/1807), Viện Hàn lâm Khoa học Pháp (1804/1820), Hội Hoàng gia Luân Đôn (1804), Viện Hàn lâm Khoa học Phổ ở Berlin (1810), Viện Hàn lâm Khoa học Quốc gia ở Verona (1810), Hội Hoàng gia Edinburgh (1820), Viện Hàn lâm Khoa học và Nhân văn Bayern ở Munich (1820), Viện Hàn lâm Khoa học và Văn học Hoàng gia Đan Mạch ở Copenhagen (1821), Hội Thiên văn Hoàng gia ở London (1821), Viện Hàn lâm Khoa học Hoàng gia Thụy Điển (1821), Viện Hàn lâm Khoa học và Nghệ thuật Hoa Kỳ ở Boston (1822), Hội Khoa học Hoàng gia Bohemia ở Prague (1833), Viện Hàn lâm Khoa học, Văn học và Mỹ thuật Hoàng gia Bỉ (1841/1845), Hội Khoa học Hoàng gia Uppsala (1843), Viện Hàn lâm Hoàng gia Ireland ở Dublin (1843), Viện Hoàng gia Hà Lan (1845/1851), Viện Hàn lâm Khoa học Hoàng gia Tây Ban Nha ở Madrid (1850), Hội Địa lý Nga (1851), Viện Hàn lâm Khoa học Hoàng gia ở Vienna (1848), Hội Triết học Hoa Kỳ (1853), Hội Triết học Cambridge, và Hội Khoa học Hoàng gia Hà Lan ở Haarlem.
Cả Đại học Kazan và Khoa Triết học của Đại học Karl ở Prague đều bổ nhiệm ông làm thành viên danh dự vào năm 1848.
Gauss đã nhận được Giải Lalande từ Viện Hàn lâm Khoa học Pháp vào năm 1809 cho lý thuyết về các hành tinh và phương tiện xác định quỹ đạo của chúng chỉ từ ba quan sát, giải thưởng của Viện Hàn lâm Khoa học Đan Mạch vào năm 1823 cho chuyên luận của ông về phép chiếu đồng dạng, và Huy chương Copley từ Hội Hoàng gia vào năm 1838 cho "các phát minh và nghiên cứu toán học của ông trong từ học".
Gauss được bổ nhiệm làm Hiệp sĩ của Bắc Đẩu Bội tinh Pháp vào năm 1837, và được xem là một trong những thành viên đầu tiên của Huân chương Pour le Mérite của Phổ (hạng dân sự) khi nó được thành lập vào năm 1842. Ông đã nhận được Huân chương Vương miện Westphalia (1810), Huân chương Dannebrog của Đan Mạch (1817), Huân chương Guelphic Hoàng gia của Hannover (1815), Huân chương Bắc Cực của Thụy Điển (1844), Huân chương Henry Sư tử (1849), và Huân chương Maximilian Bayern về Khoa học và Nghệ thuật (1853).
Các vị vua của Hannover đã phong cho ông các danh hiệu danh dự "Hofrath" (1816) và "Geheimer Hofrath" (tạm dịch: Cố vấn bí mật của Triều đình) (1845). Năm 1949, nhân dịp lễ kỷ niệm bằng tiến sĩ vàng của ông, ông đã được trao công dân danh dự của cả hai thành phố Brunswick và Göttingen. Ngay sau khi ông qua đời, một huy chương đã được phát hành theo lệnh của Vua George V của Hannover với dòng chữ khắc ở mặt sau dành tặng "cho Hoàng tử của các nhà toán học".
"Gauss-Gesellschaft Göttingen" ("Hội Gauss Göttingen") được thành lập vào năm 1964 để nghiên cứu cuộc đời và công trình của Carl Friedrich Gauss và những người liên quan, đồng thời xuất bản Mitteilungen der Gauss-Gesellschaft (Thông báo của Hội Gauss).
4. Các tác phẩm chọn lọc
Các tác phẩm của Johann Carl Friedrich Gauss bao gồm nhiều sách, bài báo và thư từ quan trọng trong các lĩnh vực toán học, thiên văn học và vật lý.
4.1. Toán học và thiên văn học

- 1799: Demonstratio nova theorematis omnem functionem algebraicam rationalem integram unius variabilis in factores reales primi vel secundi gradus resolvi posse (Luận án tiến sĩ về định lý cơ bản của đại số, Đại học Helmstedt)
- 1800: Berechnung des Osterfestes (Tính toán ngày lễ Phục sinh)
- 1801: Disquisitiones Arithmeticae
- 1802: Berechnung des jüdischen Osterfestes (Tính toán ngày lễ Phục sinh của người Do Thái)
- 1804: Über die Grenzen der geocentrischen Oerter der Planeten (Về giới hạn của các vị trí địa tâm của các hành tinh) (về Zodiacus)
- 1808: Theorematis arithmetici demonstratio nova (Giới thiệu bổ đề Gauss, sử dụng nó trong chứng minh thứ ba của tương hỗ bậc hai)
- 1808: Methodus peculiaris elevationem poli determinandi
- 1809: Theoria motus corporum coelestium in sectionibus conicis solem ambientium (Lý thuyết về chuyển động của các thiên thể di chuyển quanh Mặt Trời trong các mặt cắt hình nón)
- 1811: Disquisitio de elementis ellipticis Palladis ex oppositionibus annorum 1803, 1804, 1805, 1806, 1807, 1808, 1809 (Quỹ đạo của Pallas)
- 1811: Summatio quarundam serierum singularium (Xác định dấu của tổng Gauss bậc hai, sử dụng giá trị này để đưa ra chứng minh thứ tư của tương hỗ bậc hai)
- 1813: Disquisitiones generales circa seriem infinitam (từ 1812, chứa phân số liên tục Gauss)
- 1816: Methodus nova integralium valores per approximationem inveniendi (từ 1814)
- 1816: Demonstratio nova altera theorematis omnem functionem algebraicam rationalem integram unius variabilis in factores reales primi vel secundi gradus resolvi posse
- 1816: Theorematis de resolubilitate functionum algebraicarum integrarum in factores reales demonstratio tertia
- 1818: Theorematis fundamentalis in doctrina de residuis quadraticis demonstrationes et ampliationes novae (từ 1817) (Chứng minh thứ năm và thứ sáu của tương hỗ bậc hai)
- 1818: Determinatio attractionis, quam in punctum positionis datae exerceret planeta, si eius massa per totamorbitam, ratione temporis, quo singulae partes describuntur, uniformiter esset dispertita (Chỉ tham chiếu đến công trình - hầu hết chưa được công bố - về thuật toán trung bình cộng-hình học.)
- 1823: Theoria combinationis observationum erroribus minimis obnoxiae. Pars Prior (từ 1821)
- 1823: Theoria combinationis observationum erroribus minimis obnoxiae. Pars Posterior
- 1825: Allgemeine Auflösung der Aufgabe die Theile einer gegebnen Fläche auf einer andern gegebnen Fläche so abzubilden dass die Abbildung dem Abgebildeten in den kleinsten Theilen ähnlich wird (Bài tiểu luận đoạt giải từ 1822 về ánh xạ bảo giác)
- 1828: Bestimmung des Breitenunterschiedes zwischen den Sternwarten von Göttingen und Altona durch Beobachtungen am Ramsdenschen Zenithsector (Xác định sự khác biệt về vĩ độ giữa các đài thiên văn Göttingen và Altona bằng các quan sát với kính thiên văn Ramsden)
- 1828: Supplementum theoriae combinationis observationum erroribus minimis obnoxiae (từ 1826)
- 1828: Disquisitiones generales circa superficies curvas (từ 1827)
- 1828: Theoria residuorum biquadraticorum, Commentatio prima (từ 1825)
- 1832: Theoria residuorum biquadraticorum, Commentatio secunda (từ 1831) (Giới thiệu các số nguyên Gauss, nêu (không có chứng minh) định luật tương hỗ bậc bốn, chứng minh luật bổ sung cho 1 + i)
- 1845: Untersuchungen über Gegenstände der Höheren Geodäsie. Erste Abhandlung (từ 1843)
- 1847: Untersuchungen über Gegenstände der Höheren Geodäsie. Zweite Abhandlung (từ 1846)
- 1848: Schreiben des Herrn Geheimen Hofrathes Gauss an den Herausgeber (Thư của Cố vấn bí mật của Triều đình Gauss gửi biên tập viên)
- 1850: Beiträge zur Theorie der algebraischen Gleichungen (Bài giảng từ 1849)
- 1903: Wissenschaftliches Tagebuch (Nhật ký khoa học) (từ 1847, về Zodiacus)
4.2. Vật lý
- 1804: Fundamentalgleichungen für die Bewegung schwerer Körper auf der Erde (trong sách gốc: Versuche über das Gesetz des Falls, über den Widerstand der Luft und über die Umdrehung der Erde)
- 1813: Theoria attractionis corporum sphaeroidicorum ellipticorum homogeneorum methodo nova tractata (chứa định lý Gauss của giải tích vector)
- 1817: Ueber die achromatischen Doppelobjective besonders in Rücksicht der vollkommnern Aufhebung der Farbenzerstreuung (Về các thấu kính kép sắc nét đặc biệt liên quan đến việc loại bỏ hoàn toàn sự tán sắc màu)
- 1829: Über ein neues allgemeines Grundgesetz der Mechanik (Về một định luật cơ bản chung mới của cơ học)
- 1830: Principia generalia theoriae figurae fluidorum in statu aequilibrii (từ 1829)
- 1836: Erdmagnetismus und Magnetometer (Địa từ học và từ kế)
- 1840: Allgemeine Lehrsätze in Beziehung auf die im verkehrten Verhältnis des Quadrats der Entfernung wirkenden Anziehungs- und Abstoßungskräfte (Các định lý chung liên quan đến các lực hấp dẫn và đẩy tác dụng theo tỷ lệ nghịch của khoảng cách bậc hai)
- 1841: Intensitas vis magneticae terrestris ad mensuram absolutam revocata (từ 1832) (Cường độ của lực từ Trái Đất được quy về đo lường tuyệt đối)
- 1843: Dioptrische Untersuchungen (Nghiên cứu khúc xạ) (từ 1840)
4.2.1. Cùng với Wilhelm Weber
- 1837-1839: Resultate aus den Beobachtungen des magnetischen Vereins im Jahre 1836-1838
- 1840-1843: Resultate aus den Beobachtungen des magnetischen Vereins im Jahre 1839-1841
- 1840: Atlas des Erdmagnetismus nach den Elementen der Theorie entworfen. Supplement zu den Resultaten aus den Beobachtungen des magnetischen Vereins
4.3. Thư từ
Viện Hàn lâm Khoa học Göttingen cung cấp một bộ sưu tập đầy đủ các lá thư đã biết từ và gửi đến Carl Friedrich Gauss có thể truy cập trực tuyến. Di sản văn học được lưu giữ và cung cấp bởi Thư viện Bang và Đại học Göttingen. Các tài liệu viết từ Carl Friedrich Gauss và các thành viên gia đình cũng có thể được tìm thấy trong kho lưu trữ thành phố Brunswick.
Các bộ sưu tập thư từ đáng chú ý bao gồm:
- Thư từ giữa Gauss và Bessel (tháng 12 năm 1804 đến tháng 8 năm 1844)
- Thư từ chưa biết của C. F. Gauss và Fr. W. Bessel (thư gửi Boguslawski từ tháng 2 năm 1835 đến tháng 1 năm 1848)
- Thư từ giữa Carl Friedrich Gauss và Johann Elert Bode (tháng 2 năm 1802 đến tháng 10 năm 1826)
- Thư từ giữa Carl Friedrich Gauss và Wolfgang Bolyai (tháng 9 năm 1797 đến tháng 2 năm 1853; thêm thư từ các người khác)
- Thư từ giữa Carl Friedrich Gauss và Johann Franz Encke (tháng 6 năm 1810 đến tháng 6 năm 1854)
- Thư từ giữa Carl Friedrich Gauss và Christian Ludwig Gerling (tháng 6 năm 1810 đến tháng 6 năm 1854)
- Thư từ giữa A. v. Humboldt và Gauss (tháng 7 năm 1807 đến tháng 12 năm 1854; thêm thư từ các người khác)
- Karl Kreil và địa từ học. Thư từ của ông với Carl Friedrich Gauß trong bối cảnh lịch sử (thư từ 1835 đến 1843)
- Thư từ giữa Carl Friedrich Gauß và Carl Ludwig von Lecoq (tháng 2 năm 1799 đến tháng 9 năm 1800)
- Thư từ giữa Carl Friedrich Gauss và Mục sư Nevil Maskelyne (1802-05)
- Thư từ giữa Olbers và Gauss: Phần một (tháng 1 năm 1802 đến tháng 10 năm 1819)
- Thư từ giữa Olbers và Gauss: Phần hai (tháng 1 năm 1820 đến tháng 5 năm 1839; thêm thư từ các người khác)
- Thư từ giữa C. F. Gauss và H. C. Schumacher (tháng 4 năm 1808 đến tháng 11 năm 1850)
- Thư từ giữa Carl Friedrich Gauß và Eberhard August Zimmermann (1795 đến 1815)
5. Các hoạt động tưởng niệm

Hội Gauss Göttingen (Gauss-Gesellschaft Göttingen) được thành lập vào năm 1964 để nghiên cứu cuộc đời và công trình của Carl Friedrich Gauss và những người liên quan.
Từ năm 1989 đến 2001, chân dung của Gauss, một đường cong phân phối chuẩn và một số tòa nhà nổi tiếng của Göttingen được in trên tờ tiền giấy 10 mark Đức. Mặt trái tờ tiền có in loại kính lục phân yêu thích của Gauss, cùng bản đồ Hannover. Đức cũng đã phát hành ba con tem bưu chính vinh danh Gauss. Một con tem (số 725) phát hành năm 1955 nhân kỷ niệm một trăm năm ngày mất của ông; hai con khác, mang số 1246 và 1811, phát hành năm 1977, kỷ niệm 200 năm ngày sinh của ông.
Tiểu thuyết Die Vermessung der Welt năm 2005 của Daniel Kehlmann, được dịch sang tiếng Anh là Measuring the World (2006), khám phá cuộc sống và công việc của Gauss qua lăng kính tiểu thuyết lịch sử, đối chiếu chúng với nhà thám hiểm người Đức Alexander von Humboldt. Một phiên bản phim của đạo diễn Detlev Buck đã được phát hành vào năm 2012.
Vào năm 2007, một bức tượng bán thân của Gauss đã được đặt trong đền Walhalla.
Nhiều sự vật được đặt theo tên của Gauss, bao gồm:
- Phân phối chuẩn, còn được gọi là phân phối Gauss, đường cong hình chuông phổ biến nhất trong thống kê.
- Giải thưởng Carl Friedrich Gauss, một trong những giải thưởng cao quý nhất trong toán học.
- gauss, đơn vị CGS cho từ trường.
- Tiểu hành tinh Gaussia (1001 Gaussia), được đặt tên để vinh danh ông.
Năm 1929, nhà toán học người Ba Lan Marian Rejewski, người đã giúp giải được thuật toán của bộ máy mật mã Enigma vào tháng 12 năm 1932, bắt đầu nghiên cứu thống kê bảo hiểm tại Göttingen. Theo yêu cầu của giáo sư Đại học Poznań, Zdzisław Krygowski, khi đến Göttingen, Rejewski đã đặt hoa trên mộ của Gauss.
Ngày 30 tháng 4 năm 2018, Google đã vinh danh Gauss trong sinh nhật lần thứ 241 của mình với một Google Doodle được trưng bày ở Châu Âu, Nga, Israel, Nhật Bản, Đài Loan, một phần của Nam và Trung Mỹ và Hoa Kỳ.
Carl Friedrich Gauss, người cũng đã giới thiệu cái gọi là logarit Gauss, đôi khi bị nhầm lẫn với Friedrich Gustav GaußFriedrich Gustav GaussGerman (1829-1915), một nhà địa chất người Đức, người cũng đã xuất bản một số bảng logarit nổi tiếng được sử dụng vào đầu những năm 1980.