Omar Khayyám

1.1. Sinh và thời thơ ấu

Khayyam trải qua thời thơ ấu tại Nishapur, nơi từng là một trung tâm quan trọng của Hỏa giáo. Theo nhà sử học Bayhaqi, người quen biết cá nhân với Khayyam, ông thuộc cung Song Tử với mặt trời và sao Thủy ở thế thượng phong. Chi tiết này đã giúp các học giả hiện đại xác định ngày sinh của ông là 18 tháng 5 năm 1048.

1.2. Giáo dục

Tài năng của Khayyam sớm được các gia sư đầu tiên của ông công nhận. Họ đã gửi ông đến học với Imam Muwaffaq Nishaburi, giáo viên vĩ đại nhất vùng Khorasan, người chuyên dạy dỗ con em các quý tộc cấp cao nhất. Khayyam và Imam Muwaffaq đã phát triển một tình bạn bền chặt qua nhiều năm. Khayyam cũng có thể đã học cùng hoặc dưới sự hướng dẫn của Bahmanyar, một môn đệ của Avicenna. Ông đã theo học các ngành khoa học, triết học, toán học và thiên văn học tại Nishapur.

1.3. Sự nghiệp ban đầu và du hành

Khoảng năm 1068, sau khi hoàn tất việc học tại Nishapur, ông đi đến tỉnh Bukhara, nơi ông thường xuyên lui tới thư viện danh tiếng của Ark. Khoảng năm 1070, ông chuyển đến Samarkand, nơi ông bắt đầu biên soạn công trình nổi tiếng của mình về đại số, "Chuyên luận về Trình bày Các vấn đề của Đại số" dưới sự bảo trợ của Abu Tahir Abd al-Rahman ibn ʿAlaq, thống đốc và thẩm phán trưởng của thành phố. Khayyam được Shams al-Mulk Nasr, người cai trị Karakhanid, đón tiếp nồng hậu. Bayhaqi kể rằng Nasr "thể hiện với ông niềm vinh dự to lớn nhất, đến nỗi ông sẽ cho [Khayyam] ngồi cạnh mình trên ngai vàng".

1.4. Hoạt động dưới triều đại Seljuk

Vào năm 1074, sau khi hòa bình được ký kết với Sultan Malik-Shah I, người đã tiến hành các cuộc xâm nhập vào lãnh địa của Karakhanid, Khayyam đã nhận lời mời của Đại Tể tướng Nizam al-Mulk đến Marv để phục vụ Malik-Shah. Ông sau đó được giao nhiệm vụ xây dựng một đài quan sát ở Isfahan và lãnh đạo một nhóm các nhà khoa học thực hiện các quan sát thiên văn chính xác nhằm cải cách lịch Ba Tư. Công việc này bắt đầu vào khoảng năm 1076 và kết thúc vào năm 1079, khi Khayyam và các đồng nghiệp hoàn tất các phép đo độ dài của năm, báo cáo là 365,24219858156 ngày.

1.5. Khám phá triết học và tôn giáo

Sau cái chết của Malik-Shah và tể tướng của ông (được cho là bị ám sát bởi sát thủ Ismaili), Khayyam mất đi sự ưu ái của triều đình. Điều này đã thúc đẩy ông sớm thực hiện một chuyến hành hương đến Mecca. Một động cơ tiềm ẩn cho chuyến đi này, theo Al-Qifti, có thể là để công khai chứng tỏ đức tin của mình, xoa dịu những nghi ngờ về chủ nghĩa hoài nghi và bác bỏ các cáo buộc không chính thống (bao gồm cả khả năng có thiện cảm hoặc tuân thủ Hỏa giáo) từ giới giáo sĩ thù địch.

1.6. Hành hương đến Mecca

Chuyến hành hương của Khayyam đến Mecca, mặc dù có thể là để chứng minh lòng mộ đạo của ông trước những cáo buộc, cũng thể hiện một phần sự phức tạp trong quan điểm tôn giáo của ông. Theo các tài liệu, sau khi trở về quê nhà Nishapur, ông đã che giấu những niềm tin sâu sắc nhất của mình và tuân thủ một lối sống tôn giáo nghiêm ngặt, thường xuyên đến nơi thờ phượng. Tuy nhiên, các tác phẩm triết học và thơ ca của ông vẫn cho thấy một tinh thần tự do và tư duy phản biện mạnh mẽ, thường xuyên đặt câu hỏi về các giáo điều và định mệnh.

1.7. Cuối đời và cái chết

Sau chuyến hành hương, Khayyam được Sultan Sanjar mời đến Marv, có lẽ để làm chiêm tinh của triều đình, một công việc mà ông dường như không làm tốt. Sau đó, ông được phép trở về Nishapur do sức khỏe suy giảm. Khi trở về, ông dường như đã sống một cuộc đời ẩn dật.

Omar Khayyam qua đời ở tuổi 83 tại quê nhà Nishapur vào ngày 4 tháng 12 năm 1131. Ông được chôn cất tại nơi hiện nay là Lăng mộ Omar Khayyam.

1.8. Lăng mộ

Một trong những môn đệ của ông, Nizami Aruzi, kể lại câu chuyện rằng vào khoảng năm 1112-1113, Khayyam đang ở Balkh cùng với Al-Isfizari (một nhà khoa học từng hợp tác với ông trong dự án lịch Jalali) khi ông tiên đoán rằng "ngôi mộ của ta sẽ ở một nơi mà gió bắc có thể rải hoa hồng lên đó". Bốn năm sau khi ông qua đời, Aruzi đã tìm thấy ngôi mộ của ông trong một nghĩa trang ở một khu vực rộng lớn và nổi tiếng của Nishapur, trên con đường đến Marv. Đúng như Khayyam đã dự đoán, Aruzi thấy ngôi mộ nằm dưới chân một bức tường vườn, nơi những cây lê và cây mơ vươn cành và rụng hoa, che phủ bia mộ của ông. Hình dáng kiến trúc lăng mộ của ông sau này được xây dựng giống như một chiếc lều, gợi nhớ đến nghề làm lều của tổ tiên ông. Một số bài tứ tuyệt của ông được sử dụng làm trang trí thư pháp (thư pháp taliq) trên phần ngoại thất của lăng mộ.

2.1. Đại số hình học và giải phương trình bậc ba

Rashed và Vahabzadeh (2000) đã lập luận rằng, nhờ cách tiếp cận hình học triệt để đối với các phương trình đại số, Khayyam có thể được coi là tiền thân của Descartes trong việc phát minh ra hình học giải tích. Trong "Chuyên luận về Phép chia góc phần tư của hình tròn", Khayyam đã áp dụng đại số vào hình học. Trong tác phẩm này, ông chủ yếu tập trung nghiên cứu khả năng chia một góc phần tư hình tròn thành hai phần sao cho các đoạn thẳng chiếu từ điểm chia đến các đường kính vuông góc của hình tròn tạo thành một tỷ lệ cụ thể. Giải pháp của ông đã sử dụng nhiều phép xây dựng đường cong dẫn đến các phương trình chứa các số hạng bậc ba và bậc bốn.

Khayyam dường như là người đầu tiên đưa ra một lý thuyết tổng quát về phương trình bậc ba và là người đầu tiên giải quyết bằng hình học mọi loại phương trình bậc ba, xét về các nghiệm dương. "Chuyên luận về Đại số" của ông chứa đựng công trình về phương trình bậc ba. Nó được chia thành ba phần: (i) các phương trình có thể giải bằng compa và thước thẳng, (ii) các phương trình có thể giải bằng đường conic, và (iii) các phương trình liên quan đến nghịch đảo phép nhân của ẩn số.

Khayyam đã lập một danh sách đầy đủ tất cả các phương trình có thể có liên quan đến đường thẳng, hình vuông và hình lập phương. Ông xem xét ba phương trình nhị thức, chín phương trình tam thức và bảy phương trình tứ thức. Đối với các đa thức bậc nhất và bậc hai, ông cung cấp các nghiệm số bằng cách xây dựng hình học. Ông kết luận rằng có mười bốn loại hình khối khác nhau không thể rút gọn thành phương trình bậc thấp hơn. Đối với những loại này, ông không thể hoàn thành việc xây dựng đoạn thẳng ẩn số của mình bằng compa và thước thẳng. Ông tiếp tục trình bày các giải pháp hình học cho tất cả các loại phương trình bậc ba bằng cách sử dụng các tính chất của các hình nón conic. Nghiệm dương của một phương trình bậc ba được xác định là trục hoành của giao điểm của hai đường conic, ví dụ, giao điểm của hai parabol, hoặc giao điểm của một parabol và một đường tròn. Tuy nhiên, ông thừa nhận rằng vấn đề số học của các hình khối này vẫn chưa được giải quyết, và nói thêm rằng "có thể ai đó khác sẽ biết được nó sau chúng ta". Nhiệm vụ này vẫn còn bỏ ngỏ cho đến thế kỷ 16, khi một giải pháp đại số tổng quát cho phương trình bậc ba được Cardano, Del Ferro và Tartaglia tìm ra ở Phục hưng Ý.

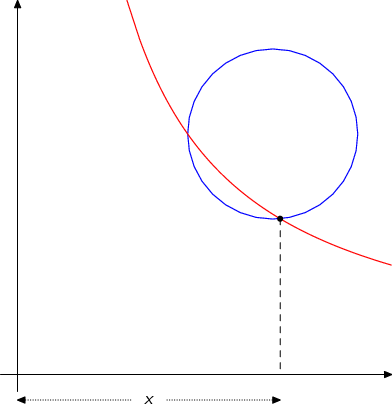
Công trình của Khayyam là một nỗ lực nhằm thống nhất đại số và hình học. Cách giải hình học cụ thể này của phương trình bậc ba đã được M. Hachtroudi nghiên cứu sâu hơn và mở rộng để giải các phương trình bậc bốn. Mặc dù các phương pháp tương tự đã xuất hiện lẻ tẻ từ thời Menaechmus và được phát triển thêm bởi nhà toán học thế kỷ 10 Abu al-Jud, công trình của Khayyam có thể được coi là nghiên cứu có hệ thống đầu tiên và phương pháp chính xác đầu tiên để giải các phương trình bậc ba. Nhà toán học Woepcke (1851), người đã dịch đại số của Khayyam sang tiếng Pháp, đã ca ngợi ông vì "sức mạnh khái quát hóa và quy trình hệ thống chặt chẽ của ông".

2.2. Lý thuyết về đường song song

Một phần của "Một nhận xét về các khó khăn liên quan đến các mệnh đề trong cuốn Các nguyên tố của Euclid" của Khayyam đề cập đến tiên đề song song. Chuyên luận của Khayyam có thể được coi là bản thảo đầu tiên về tiên đề này không dựa trên petitio principii (lỗi ngộ nhận), mà dựa trên một mệnh đề trực quan hơn. Khayyam bác bỏ các nỗ lực trước đó của các nhà toán học khác nhằm "chứng minh" mệnh đề, chủ yếu vì lý do là mỗi người trong số họ đã giả định một điều gì đó không hề dễ chấp nhận hơn chính Tiên đề thứ năm. Dựa trên quan điểm của Aristoteles, ông từ chối việc sử dụng chuyển động trong hình học và do đó bác bỏ nỗ lực khác của Ibn al-Haytham. Không hài lòng với sự thất bại của các nhà toán học trong việc chứng minh tuyên bố của Euclid từ các định đề khác của ông, Khayyam đã cố gắng kết nối tiên đề với Tiên đề thứ tư, nói rằng tất cả các góc vuông đều bằng nhau.

Khayyam là người đầu tiên xem xét ba trường hợp riêng biệt của góc nhọn, góc tù và góc vuông cho các góc đỉnh của một tứ giác Khayyam-Saccheri. Sau khi chứng minh một số định lý về chúng, ông chỉ ra rằng Tiên đề V tuân theo giả thuyết góc vuông, và bác bỏ các trường hợp góc tù và góc nhọn là tự mâu thuẫn. Nỗ lực công phu của ông để chứng minh tiên đề song song có ý nghĩa quan trọng đối với sự phát triển hơn nữa của hình học, vì nó cho thấy rõ ràng khả năng của hình học phi Euclid. Các giả thuyết về góc nhọn, góc tù và góc vuông hiện nay được biết là dẫn đến hình học hyperbolic của Gauss-Bolyai-Lobachevsky, hình học Riemann, và hình học Euclid tương ứng.

Các bình luận của Tusi về cách Khayyam xử lý các đường song song đã đến châu Âu. John Wallis, giáo sư hình học tại Oxford, đã dịch bình luận của Tusi sang tiếng Latinh. Nhà hình học dòng Jesuit Girolamo Saccheri, người có tác phẩm (Euclides ab omni naevo vindicatus, 1733) thường được coi là bước đầu tiên trong sự phát triển cuối cùng của hình học phi Euclid, đã quen thuộc với công trình của Wallis. Nhà sử học toán học người Mỹ David Eugene Smith đề cập rằng Saccheri "đã sử dụng cùng một bổ đề như của Tusi, thậm chí còn ký hiệu hình học chính xác theo cùng một cách và sử dụng bổ đề cho cùng mục đích." Ông nói thêm rằng "Tusi đã nói rõ ràng rằng đó là do Omar Khayyam, và từ văn bản, có vẻ như rõ ràng rằng Khayyam là người đã truyền cảm hứng cho ông."

2.3. Khái niệm số thực

Chuyên luận này về Euclid chứa một đóng góp khác liên quan đến lý thuyết về tỷ lệ và sự kết hợp của các tỷ lệ. Khayyam thảo luận về mối quan hệ giữa khái niệm tỷ lệ và khái niệm số và nêu rõ nhiều khó khăn lý thuyết khác nhau. Cụ thể, ông đóng góp vào nghiên cứu lý thuyết về khái niệm số vô tỉ. Không hài lòng với định nghĩa của Euclid về các tỷ số bằng nhau, ông đã định nghĩa lại khái niệm về một số bằng cách sử dụng một phân số liên tục làm phương tiện biểu thị tỷ số. Adolph P. Yushkevich và Rosenfeld lập luận rằng "bằng cách đặt các đại lượng và số vô tỉ trên cùng một thang đo hoạt động, [Khayyam] đã bắt đầu một cuộc cách mạng thực sự trong học thuyết về số." Tương tự, D. J. Struik đã lưu ý rằng Omar đang "trên con đường mở rộng khái niệm số dẫn đến khái niệm về số thực."

2.4. Định lý nhị thức và khai căn

Trong chuyên luận đại số của mình, Khayyam ám chỉ đến một cuốn sách ông đã viết về việc khai thác căn bậc n của các số tự nhiên bằng cách sử dụng một định luật mà ông đã khám phá ra, không phụ thuộc vào các hình học. Cuốn sách này có thể có tựa đề là "Những khó khăn của số học" (Mushkilāt al-Ḥisāb^Arabic), nhưng hiện đã bị thất lạc. Dựa trên ngữ cảnh, một số nhà sử học toán học như D. J. Struik tin rằng Omar hẳn đã biết công thức cho khai triển (a+b)ⁿ, trong đó n là một số nguyên dương. Trường hợp lũy thừa 2 được nêu rõ trong cuốn "Các nguyên tố" của Euclid và trường hợp tối đa lũy thừa 3 đã được các nhà toán học Ấn Độ thiết lập. Khayyam là nhà toán học đã nhận ra tầm quan trọng của một định lý nhị thức tổng quát. Lập luận ủng hộ cho việc Khayyam có một định lý nhị thức tổng quát dựa trên khả năng khai căn của ông. Một trong những người tiền nhiệm của Khayyam, al-Karaji, đã khám phá ra cách sắp xếp hình tam giác của các hệ số khai triển nhị thức mà người châu Âu sau này biết đến là tam giác Pascal; Khayyam đã phổ biến cách sắp xếp hình tam giác này ở Iran, do đó nó hiện được gọi là tam giác Omar Khayyam.

:Từ những người Ấn Độ, người ta có các phương pháp để lấy căn bậc hai và căn bậc ba, các phương pháp ấy dựa trên hiểu biết về các trường hợp riêng lẻ-cụ thể là hiểu biết về các bình phương trong số chín chữ số 1², 2², 3² (v.v.) và các tích tương ứng của chúng, ví dụ 2 x 3 v.v.. Chúng ta đã viết một chuyên luận về bằng chứng cho tính hợp lệ của các phương pháp ấy và rằng chúng thực sự đáp ứng các điều kiện. Thêm vào đó, chúng ta đã gia tăng các kiểu loại của chúng, cụ thể là việc xác định các căn bậc bốn, năm, sáu, hay bất kỳ bậc mong muốn nào. Chưa có ai vượt qua được chúng ta về điều này và những chứng minh đó hoàn toàn là số học, dựa trên số học của cuốn "Các nguyên tố" của Euclid.

3.1. Quan sát thiên văn

Một trong những học trò của ông, Nizami Aruzi, kể lại rằng Khayyam rõ ràng không có niềm tin lớn vào chiêm tinh học và bói toán. Aruzi chưa từng thấy hay nghe nói về bất kỳ nhà khoa học vĩ đại nào có niềm tin như vậy. Khi làm việc cho Sultan Sanjar với tư cách là một nhà chiêm tinh, ông được yêu cầu dự đoán thời tiết - một công việc mà ông dường như không làm tốt. George Saliba (2002) giải thích rằng thuật ngữ 'ilm al-nujūm^Arabic, được sử dụng trong các nguồn tư liệu tham khảo về cuộc đời và công việc của Khayyam, đôi khi bị dịch sai thành chiêm tinh học. Ông nói thêm rằng "ít nhất là từ giữa thế kỷ 10, theo cách liệt kê các ngành khoa học của Farabi, thì ngành khoa học này, 'ilm al-nujūm^Arabic, đã được chia thành hai phần: một phần nghiên cứu về chiêm tinh học và phần còn lại nghiên cứu về lý thuyết toán thiên văn học."

4.1. Rubaiyat

Việc ám chỉ sớm nhất về thơ của Omar Khayyam là từ nhà sử học Imad ad-Din al-Isfahani, một người cùng thời trẻ tuổi với Khayyam, người đã gọi ông là cả nhà thơ và nhà khoa học (trong tác phẩm Kharidat al-qasr, 1174). Một trong những mẫu vật sớm nhất của Rubaiyat của Omar Khayyam là từ học giả Fakhr al-Din Razi. Trong tác phẩm Al-tanbih 'ala ba'd asrar al-maw'dat fi'l-Qur'an (khoảng năm 1160), Razi trích dẫn một trong những bài thơ của Khayyam (tương ứng với khổ tứ tuyệt LXII trong ấn bản đầu tiên của FitzGerald). Daya trong các tác phẩm của mình (Mirsad al-'Ibad, khoảng năm 1230) trích dẫn hai bài tứ tuyệt, một trong số đó giống với bài đã được Razi ghi nhận. Một bài tứ tuyệt bổ sung được trích dẫn bởi nhà sử học Juvayni (Tarikh-i Jahangushay, khoảng năm 1226-1283). Năm 1340, Jajarmi đưa mười ba bài tứ tuyệt của Khayyam vào công trình của mình, bao gồm một tuyển tập các tác phẩm của những nhà thơ Ba Tư nổi tiếng (Munis al-ahrār), hai trong số đó cho đến nay đã được biết đến từ các nguồn cũ hơn. Một bản thảo tương đối muộn là bản thảo của Thư viện Bodleian, MS. Ouseley 140, viết tại Shiraz vào năm 1460, bao gồm 158 bài tứ tuyệt trên 47 tờ. Bản thảo này thuộc về William Ouseley (1767-1842) và được Thư viện Bodleian mua lại vào năm 1844.

Đôi khi có những câu thơ được cho là của Khayyam được trích dẫn trong các văn bản của các tác giả thế kỷ 13 và 14, nhưng tính xác thực của chúng còn đáng ngờ. Các học giả hoài nghi chỉ ra rằng toàn bộ truyền thống này có thể là bút ký giả. Hans Heinrich Schaeder vào năm 1934 thậm chí đã bình luận rằng tên của Omar Khayyam "nên bị gạch khỏi lịch sử văn học Ba Tư" do thiếu các tài liệu có thể tự tin gán cho ông. François De Blois (2004) cũng kết luận một cách bi quan rằng tình hình không thay đổi đáng kể kể từ thời Schaeder. Tuy nhiên, năm trong số các bài tứ tuyệt sau này được cho là của Omar đã được tìm thấy sớm nhất là 30 năm sau khi ông qua đời, được trích dẫn trong Sindbad-Nameh. Điều này chứng tỏ rằng những câu thơ này đã được lưu hành vào thời của Omar hoặc ngay sau đó, mặc dù không có nghĩa là chúng phải là của ông. De Blois kết luận rằng, ít nhất quá trình gán thơ cho Khayyam dường như đã bắt đầu từ thế kỷ 13. Edward Granville Browne (1906) cũng lưu ý khó khăn trong việc phân biệt các bài tứ tuyệt xác thực với những bài giả mạo: "mặc dù chắc chắn rằng Khayyam đã viết nhiều bài tứ tuyệt, nhưng gần như không thể, ngoại trừ một vài trường hợp ngoại lệ, khẳng định chắc chắn rằng ông đã viết bất kỳ bài thơ nào được gán cho ông".

Ngoài những bài tứ tuyệt Ba Tư, còn có 25 bài thơ Ả Rập được cho là của Khayyam. Chúng đã được chứng thực bởi các nhà sử học như al-Isfahani, Shahrazuri (Nuzhat al-Arwah, khoảng năm 1201-1211), Qifti (Tārikh al-hukamā, 1255), và Hamdallah Mustawfi (Tarikh-i guzida, 1339). Boyle nhấn mạnh rằng có một số học giả Ba Tư khác cũng thỉnh thoảng viết thơ tứ tuyệt, bao gồm Avicenna, Ghazzali và Tusi. Ông kết luận rằng có thể đối với Khayyam, thơ ca là một thú tiêu khiển trong những giờ rảnh rỗi của ông: "những bài thơ ngắn này dường như thường là tác phẩm của các học giả và nhà khoa học, những người sáng tác chúng, có lẽ, trong những giây phút thư giãn để khai sáng hoặc giải trí trong giới nội bộ các đệ tử của họ".

Thơ ca được cho là của Omar Khayyam đã góp phần rất lớn vào danh tiếng phổ biến của ông trong thời kỳ hiện đại, trực tiếp nhờ vào sự phổ biến cực kỳ của bản dịch những câu thơ đó sang tiếng Anh của Edward FitzGerald (1859). Rubaiyat của Omar Khayyam của FitzGerald chứa các bản dịch phóng khoáng từ bản thảo Bodleian. Nó đã đạt được thành công lớn trong thời kỳ fin de siècle đến nỗi một thư mục biên soạn năm 1929 đã liệt kê hơn 300 ấn bản riêng biệt, và còn nhiều ấn bản khác đã được xuất bản kể từ đó.

4.2. Tư tưởng Triết học

Khayyam tự xem mình là một học trò của Avicenna. Theo Al-Bayhaqi, ông đã đọc siêu hình học trong "Sách chữa lành" của Avicenna trước khi qua đời. Có sáu bài viết triết học được cho là của Khayyam. Một trong số đó, Về sự tồn tại (Fi'l-wujūd^Arabic), được viết bằng tiếng Ba Tư, đề cập đến chủ đề sự tồn tại và mối quan hệ của nó với các toàn thể. Một bài viết khác, có tiêu đề Sự cần thiết của mâu thuẫn trong thế giới, thuyết tất định và sự tồn sinh (Darurat al-tadād fi'l-'ālam wa'l-jabr wa'l-baqā'^Arabic), được viết bằng tiếng Ả Rập và đề cập đến ý chí tự do và thuyết tất định. Các tác phẩm khác của ông bao gồm Về sự hiện hữu và tất yếu cần thiết (Risālah fī'l-kawn wa'l-taklīf^Arabic), Chuyên luận về Sự siêu việt trong Tồn tại (Al-Risālah al-ulā fi'l-wujūd^Arabic), Về kiến thức của các nguyên tắc tồn tại phổ quát (Risālah dar 'ilm kulliyāt-i wujūd^Arabic), và Sự rút gọn liên quan đến các hiện tượng tự nhiên (Mukhtasar fi'l-Tabi'iyyāt^Arabic).

Khayyam từng bày tỏ sự thất vọng về tình trạng khoa học và triết học trong thời đại của mình:
:Chúng ta là nạn nhân của thời đại mà những con người của khoa học bị mất uy tín, và chỉ còn lại một số ít người có khả năng tham gia nghiên cứu khoa học. Các nhà triết học của chúng ta dành tất cả thời gian của họ trộn lẫn đúng với sai và chẳng quan tâm đến điều gì ngoài việc thể hiện tự phụ ngoài mặt; sự học ít ỏi như vậy mà chúng có, chúng mở rộng về mặt vật chất. Khi chúng nhìn thấy một con người chân thành và không ngừng tìm kiếm sự thật, một người mà sẽ chẳng liên quan gì đến sự lừa dối và giả tạo, chúng chế giễu và coi thường anh ta.

4.3. Quan điểm Tôn giáo

Việc đọc các bài tứ tuyệt của Khayyam theo nghĩa đen thường dẫn đến việc giải thích thái độ triết học của ông đối với cuộc sống như một sự kết hợp của chủ nghĩa bi quan, chủ nghĩa hư vô, chủ nghĩa Epicurus, thuyết định mệnh và thuyết bất khả tri. Quan điểm này được các nhà Iran học như Arthur Christensen, Hans Heinrich Schaeder, John Andrew Boyle, Edward Denison Ross, Edward Henry Whinfield và George Sarton ủng hộ. Ngược lại, các bài tứ tuyệt của Khayyam cũng được mô tả như là thơ Sufi thần bí. J. C. E. Bowen (1973) đề cập rằng các bài thơ Ả Rập của Khayyam cũng "thể hiện quan điểm bi quan hoàn toàn phù hợp với vẻ ngoài của một nhà triết học duy lý trí sâu sắc mà Khayyam được biết đến trong lịch sử." Edward FitzGerald nhấn mạnh chủ nghĩa hoài nghi tôn giáo mà ông tìm thấy ở Khayyam. Trong lời nói đầu của Rubáiyát, ông tuyên bố rằng Khayyam "bị những người Sufi căm ghét và khiếp sợ", và phủ nhận mọi ý định ngụ ngôn thần thánh, cho rằng rượu trong thơ là rượu thật, quán rượu là nơi bán rượu, và Saki là người rót rượu. Sadegh Hedayat là một trong những người ủng hộ đáng chú ý nhất của triết học Khayyam là chủ nghĩa hoài nghi bất khả tri, và theo Jan Rypka (1934), ông thậm chí còn xem Khayyam là một người vô thần. Hedayat (1923) nói rằng "trong khi Khayyam tin vào sự biến tính và chuyển đổi của cơ thể con người, ông ấy không tin vào một linh hồn riêng biệt; nếu chúng ta may mắn, các phần tử cơ thể của chúng ta sẽ được sử dụng để làm ra một bình rượu vang." Thơ ca của Omar Khayyam đã được trích dẫn trong bối cảnh của Chủ nghĩa Vô thần Mới, chẳng hạn như trong The Portable Atheist của Christopher Hitchens.

Al-Qifti (khoảng năm 1172-1248) dường như xác nhận quan điểm này về triết học của Khayyam. Trong tác phẩm Lịch sử của những Người Uyên bác, ông ghi nhận rằng các bài thơ của Khayyam chỉ mang phong cách Sufi về bề ngoài, nhưng được viết với một tư tưởng chống tôn giáo. Ông cũng đề cập rằng Khayyam đã có lúc bị truy tố vì tội bất kính, nhưng đã đi hành hương để chứng tỏ mình là người ngoan đạo. Tài liệu ghi lại rằng khi trở về quê nhà, ông đã che giấu niềm tin sâu sắc nhất của mình và thực hành một cuộc sống tôn giáo nghiêm ngặt, sáng tối đều đến nơi thờ phượng.

Các đoạn trích từ Rubaiyat thể hiện rõ tư tưởng tự do và hoài nghi của ông:
:Kinh Koran! được thôi, hãy để ta kiểm tra, Cuốn sách cũ kỹ đáng yêu với lầm lỗi đáng ghê tởm, Hãy tin ta, ta cũng có thể đọc trích dẫn kinh Koran, Kẻ không tin là người hiểu rõ kinh Koran nhất. Và ngươi có nghĩ rằng đối với những kẻ như ngươi, một đoàn người đầu óc giòi bọ, đói khát, cuồng tín, Chúa đã ban Bí mật cho ngươi và chối từ ta đó ư? Được, được, cũng chả quan trọng! Hãy cũng cứ tin như thế.

:Đừng hướng nhìn lên, chẳng có câu trả lời ở đó đâu; Đừng cầu nguyện, vì chẳng ai nghe lời cầu nguyện của nhà ngươi; Gần là gần cũng như Chúa là Xa dường nào, Và Tại đây cũng cùng sự dối lừa như Tại đó.

:Người ta nói về thiên đường,-chẳng có thiên đường nào khác ngoài ở đây; Người ta nói về địa ngục,-chẳng có địa ngục nào ngoài ở đây; Người đời sau nói chuyện, và kiếp sau, hỡi em yêu, chẳng có kiếp nào khác-ngoài kiếp này.

Một bản tường thuật về ông, được viết vào thế kỷ 13, cho thấy ông là người "thông thạo tất cả sự khôn ngoan của người Hy Lạp," và thường nhấn mạnh sự cần thiết của việc nghiên cứu khoa học theo đường lối Hy Lạp. Trong số các tác phẩm văn xuôi của ông, có hai tác phẩm nổi bật đề cập đến đá quý và khí hậu học. Rõ ràng, nhà thơ kiêm nhà thiên văn này không sùng đạo; và thiên văn học của ông chắc chắn đã góp phần vào điều đó. Một người đương thời viết: "Tôi không quan sát thấy ông ấy có bất kỳ niềm tin lớn nào vào các dự đoán chiêm tinh; tôi cũng chưa từng thấy hay nghe nói về bất kỳ (nhà khoa học) vĩ đại nào sở hữu niềm tin như vậy. Ông dành sự tuân thủ của mình cho trường phái không tôn giáo nào cả. Thuyết bất khả tri, mà không phải đức tin, là từ khoá trong các tác phẩm của ông. Trong số các giáo phái, ông thấy đầy rẫy khắp nơi những xung đột và hận thù mà ông không thể nhập cuộc...." Tiểu thuyết gia Ba Tư Sadegh Hedayat kể rằng Khayyám từ "khi còn trẻ cho đến khi qua đời vẫn là một người theo chủ nghĩa duy vật, bi quan, bất khả tri. Khayyam nhìn nhận mọi câu hỏi về tôn giáo bằng con mắt hoài nghi," Hedayat tiếp tục, "và ghét bỏ chủ nghĩa cuồng tín, hẹp hòi, và tinh thần báo thù của các giáo sĩ mulla, những người được gọi là các học giả tôn giáo."

Trong bối cảnh của một văn phẩm có tựa đề Về kiến thức của các Nguyên lý Tồn tại, Khayyam tán thành đường lối thần bí Sufi. Csillik (1960) gợi ý khả năng rằng Omar Khayyam có thể nhìn thấy ở Sufism một đồng minh chống lại tôn giáo chính thống. Các nhà bình luận khác không chấp nhận rằng thơ ca của Khayyam có tư tưởng chống tôn giáo và diễn giải những đề cập của ông đến rượu và say theo nghĩa ẩn dụ thông thường phổ biến trong Sufism. Dịch giả tiếng Pháp J. B. Nicolas cho rằng không nên hiểu việc Khayyam thường xuyên khuyến khích uống rượu theo nghĩa đen, mà hơn là nên được xem xét dưới ánh sáng của tư tưởng Sufi, theo đó cơn say cuồng nhiệt của "rượu" được hiểu như một phép ẩn dụ cho trạng thái giác ngộ hoặc sự sung sướng hân hoan thần thánh của "baqaa". Quan điểm xem Omar Khayyam là một Sufi được bảo vệ bởi Bjerregaard (1915), Idries Shah (1999), và Dougan (1991), những người cho rằng danh tiếng của chủ nghĩa khoái lạc là do những thất bại trong bản dịch của FitzGerald, lập luận rằng thơ của Khayyam nên được hiểu như một điều "bí truyền sâu sắc". Mặt khác, các chuyên gia Iran như Mohammad Ali Foroughi và Mojtaba Minovi bác bỏ giả thuyết rằng Omar Khayyam là một Sufi. Foroughi tuyên bố rằng những ý tưởng của Khayyam có thể nhất quán với tư tưởng của những người Sufi vào thời điểm đó nhưng không có bằng chứng rằng ông chính thức là một Sufi. Aminrazavi (2007) tuyên bố rằng, "Diễn giải Sufi đối với Khayyam chỉ có thể khả thi nếu như đọc kỹ và sâu Rubāʿīyyāt của ông và kéo dài nội dung cho phù hợp với học thuyết Sufi cổ điển." Hơn nữa, Frye (1975) nhấn mạnh rằng Khayyam bị một số nhà thần bí Sufi nổi tiếng cùng thế kỷ cực kỳ bất mãn, bao gồm Shams Tabrizi (người hướng đạo tinh thần của Rumi), Najm al-Din Daya, người đã mô tả Omar Khayyam là "một triết gia, người vô thần, và người theo chủ nghĩa duy vật bất hạnh," và Attar, người đã không coi ông như một đồng đạo thần bí mà là một nhà khoa học có tư tưởng tự do, người đang chờ đợi sự trừng phạt sau này.

Seyyed Hossein Nasr lập luận rằng, việc sử dụng cách diễn giải theo nghĩa đen các câu thơ của ông (nhiều câu trong số đó không chắc chắn về tính xác thực ngay từ đầu) là "đơn giản hóa" để thiết lập triết lý của Omar Khayyam. Thay vào đó, ông trích dẫn bản dịch diễn giải của Khayyam về chuyên luận của Avicenna Diễn ngôn về sự thống nhất (Al-Khutbat al-Tawhīd^Arabic), tại đó Khayyam bày tỏ các quan điểm chính thống về Sự thống nhất Thiêng liêng đồng tình với tác giả. Các tác phẩm văn xuôi được cho là của Omar được viết theo phong cách Peripatetic và rõ ràng là hữu thần, đề cập đến các chủ đề như sự tồn tại của Chúa và thần học. Như Bowen đã lưu ý, những tác phẩm này cho thấy sự tham gia của Khayyam trong các vấn đề siêu hình học hơn là vào những điều tinh tế của Sufism. Như bằng chứng cho đức tin của Khayyam và/hoặc việc tuân thủ các phong tục Hồi giáo, Aminrazavi đề cập rằng trong các chuyên luận của ông, ông đưa ra những lời chào và lời cầu nguyện, ca ngợi Chúa và Muhammad. Trong hầu hết các trích đoạn tiểu sử, ông được nhắc đến bằng những kính ngữ tôn giáo như Imam, Người bảo trợ của Đức tin (Ghīyāth al-Dīn^Arabic), và Bằng chứng của Sự thật (Hujjat al-Haqq^Arabic). Aminrazavi cũng lưu ý rằng những người viết tiểu sử ca ngợi tính cách mộ đạo của Khayyam thường tránh đề cập đến thơ của ông, trong khi những người đề cập đến thơ Khayyam lại thường không ca ngợi tính cách tôn giáo của ông. Ví dụ, theo lời kể của Al-Bayhaqi, sớm hơn trước đó vài năm so với những ghi nhận tiểu sử khác, nói về Omar như một người rất ngoan đạo, người đã tuyên xưng quan điểm chính thống cho tới giờ phút cuối cùng của mình.

Trên cơ sở tất cả các chứng cứ văn bản và tiểu sử hiện có, câu hỏi về quan điểm tôn giáo của Khayyam vẫn còn phần nào bỏ ngỏ, và kết quả là Khayyam đã nhận về cả những ghi nhận và phê bình trái chiều gay gắt.

6.1. Đánh giá đương thời

Các trích đoạn tiểu sử khác nhau đề cập đến Omar Khayyam mô tả ông là người có kiến thức khoa học và thành tựu vô song trong thời đại của mình. Nhiều người gọi ông bằng danh hiệu Vua Thông Thái (ملك الحکماء^Arabic). Shahrazuri (mất năm 1300) đánh giá cao ông là một nhà toán học, và tuyên bố rằng ông có thể được xem là "người kế tục Avicenna trong các lĩnh vực triết học khác nhau". Al-Qifti (mất năm 1248), mặc dù không đồng tình với các quan điểm của ông, vẫn thừa nhận rằng ông "có kiến thức vô song về triết học tự nhiên và thiên văn học". Mặc dù được một số nhà viết tiểu sử ca ngợi là một nhà thơ, nhưng theo John Andrew Boyle, "vẫn có thể tranh luận rằng, vị thế nhà thơ hạng nhất của Khayyam là một sự phát triển tương đối muộn."

6.2. Tiếp nhận tại phương Tây

Thomas Hyde là người châu Âu đầu tiên chú ý đến Khayyam và dịch một trong những bài thơ tứ tuyệt của ông sang tiếng Latinh (Historia religionis veterum Persarum eorumque magorum, 1700). Sự quan tâm của phương Tây đối với Ba Tư lớn dần cùng với phong trào chủ nghĩa phương Đông vào thế kỷ 19. Joseph von Hammer-Purgstall (1774-1856) đã dịch một số bài thơ của Khayyam sang tiếng Đức năm 1818, và Gore Ouseley (1770-1844) dịch sang tiếng Anh năm 1846, nhưng Khayyam vẫn còn tương đối ít được biết đến ở phương Tây cho tới sau khi cuốn sách Rubaiyat của Omar Khayyam của Edward FitzGerald được xuất bản vào năm 1859. Tác phẩm của FitzGerald lúc đầu không thành công nhưng đã được Whitley Stokes phổ biến từ năm 1861 trở đi, và tác phẩm đã được nhóm nghệ thuật Pre-Raphaelites vô cùng ngưỡng mộ. Năm 1872, FitzGerald đã cho in ấn bản thứ ba, điều này làm gia tăng sự quan tâm đến tác phẩm tại Mỹ. Đến những năm 1880, cuốn sách cực kỳ nổi tiếng trên khắp cộng đồng nói tiếng Anh, dẫn đến sự hình thành nhiều "Câu lạc bộ Omar Khayyam" và một "hội sùng bái Rubaiyat thời fin de siècle". Những bài thơ của Khayyam đã được dịch ra nhiều thứ tiếng; nhiều trong số những bản dịch gần đây chính xác hơn bản của FitzGerald.

6.3. Ảnh hưởng Văn hóa và Văn học

Bản dịch của FitzGerald là một yếu tố quan trọng trong việc khơi dậy sự quan tâm đến Khayyam với tư cách là một nhà thơ ngay cả tại quê hương Iran của ông. Sadegh Hedayat, trong Những bài ca Khayyam (Taranehha-ye Khayyam, 1934) của mình, đã giới thiệu lại di sản thơ ca của Omar cho Iran hiện đại.

Các tài năng đa dạng và các hoạt động trí tuệ của Khayyam đã thu hút nhiều nhà văn Ottoman và Thổ Nhĩ Kỳ trong suốt lịch sử. Các học giả thường xem Khayyam là một phương tiện để nâng cao năng lực thơ ca và chiều sâu trí tuệ của chính họ, tìm kiếm nguồn cảm hứng và sự công nhận từ các tác phẩm của ông. Đối với nhiều nhà cải cách Hồi giáo, các câu thơ của Khayyam là một điểm đối lập với các chuẩn mực bảo thủ thịnh hành trong các xã hội Hồi giáo, tạo không gian cho tư duy độc lập và lối sống tự do. Các nhân vật như Abdullah Cevdet, Rıza Tevfik, và Yahya Kemal đã sử dụng các chủ đề của Khayyam để biện minh cho các ý thức hệ tiến bộ của họ hoặc để ca ngợi các khía cạnh tự do trong cuộc sống của họ, miêu tả ông như một hình mẫu văn hóa, chính trị và trí tuệ, người đã chứng minh sự tương thích của Hồi giáo với các quy ước hiện đại. Tương tự, các nhà thơ và trí thức cánh tả Thổ Nhĩ Kỳ, bao gồm Nâzım Hikmet, Sabahattin Eyüboğlu, A. Kadir, và Gökçe, đã sử dụng Khayyam để bảo vệ thế giới quan xã hội chủ nghĩa của họ, truyền cho giọng thơ ông một âm hưởng nhân văn trong ngôn ngữ bản địa. Sự hồi sinh của Khayyam trong tiếng Thổ Nhĩ Kỳ nói từ những năm 1980 đã biến ông thành một nhà thơ của nhân dân, với nhiều sách và bản dịch làm sống lại ý nghĩa lịch sử của ông. Ngược lại, các học giả như Dāniş, Tevfik, và Gölpınarlı đã ủng hộ việc phê bình nguồn và xác định các bài tứ tuyệt đích thực để nhận ra Khayyam chân chính giữa các nhận thức lịch sử về hình ảnh xã hội-văn hóa của ông.

6.4. Tưởng niệm và Di sản

Dưới triều đại Pahlavi, một tượng đài mới làm từ đá cẩm thạch trắng do kiến trúc sư Houshang Seyhoun thiết kế đã được dựng lên trên lăng mộ của ông. Một bức tượng của Abolhassan Sadighi đã được dựng lên ở Công viên Laleh, Tehran vào những năm 1960, và một bức tượng bán thân của cùng nhà điêu khắc đặt gần lăng mộ Khayyam ở Nishapur. Năm 2009, nhà nước Iran đã quyên tặng một tòa đài điêu khắc cho Văn phòng Liên hợp quốc tại Vienna, khánh thành tại Trung tâm Quốc tế Vienna. Năm 2016, ba bức tượng của Khayyam được khánh thành: một ở Đại học Oklahoma, một ở Nishapur và một ở Florence, Ý. Hơn 150 nhà soạn nhạc đã sử dụng Rubaiyat làm nguồn cảm hứng của họ. Nhà soạn nhạc đầu tiên như vậy là Liza Lehmann.

FitzGerald đã chuyển tên của Omar thành "Người làm túp lều", và cái tên được Anh ngữ hóa "Omar, người làm túp lều (Omar the Tentmaker)" đã gây được tiếng vang trong văn hóa đại chúng nói tiếng Anh trong một thời gian. Do đó, Nathan Haskell Dole đã xuất bản một cuốn tiểu thuyết có tên Omar, Người làm túp lều: Một chuyện tình Ba Tư Cũ vào năm 1898. Omar, Người làm túp lều của Naishapur là một cuốn tiểu thuyết lịch sử của John Smith Clarke, xuất bản năm 1910. "Omar the Tentmaker" cũng là tựa đề của một vở kịch năm 1914 do Richard Walton Tully lấy bối cảnh phương Đông, được chuyển thể thành phim câm năm 1922. Tướng Hoa Kỳ Omar Bradley được đặt cho biệt danh "Omar Người làm túp lều" trong Thế chiến thứ hai.

Nhà văn người Pháp gốc Li-băng Amin Maalouf đã dựa vào ông để viết nửa đầu cuốn tiểu thuyết hư cấu lịch sử Samarkand về cuộc đời của Khayyam và quá trình tạo ra Rubaiyat của ông. Nhà điêu khắc Eduardo Chillida đã tạo ra bốn tác phẩm bằng sắt khổng lồ mang tên Mesa de Omar Khayyam (Bàn của Omar Khayyam) vào những năm 1980.

Hố Mặt trăng Omar Khayyam được đặt tên để vinh danh ông vào năm 1970, cũng như tiểu hành tinh 3095 Omarkhayyam được nhà thiên văn Liên Xô Lyudmila Zhuravlyova phát hiện vào năm 1980.

Google đã phát hành hai Google Doodles để tưởng nhớ ông. Lần đầu tiên là vào sinh nhật lần thứ 964 của ông vào ngày 18 tháng 5 năm 2012. Lần thứ hai là vào sinh nhật lần thứ 971 của ông vào ngày 18 tháng 5 năm 2019.

6.5. Bài tứ tuyệt Ngón tay chuyển động (The Moving Finger)

Bài thơ tứ tuyệt của Omar Khayyam được biết đến với tên gọi "Ngón tay Chuyển động" (The Moving Finger), theo bản dịch của nó bởi nhà thơ người Anh Edward FitzGerald là một trong những bài tứ tuyệt nổi tiếng nhất trong vùng ngôn ngữ tiếng Anh. Thơ rằng:
:The Moving Finger writes; and having writ,
:Moves on: nor all your Piety nor Wit
:Shall lure it back to cancel half a Line,
:Nor all your Tears wash out a Word of it.

:Dịch nghĩa:
:Ngón tay cứ việc Dời chuyển; mệnh lệnh cứ thế ban ra,
:Cứ tiếp bước: chẳng phải tất cả Đạo Đức hay Thông Thái của ngươi
:Sẽ đuổi nó trở lại dừng nửa dòng,
:Tất cả Nước mắt của ngươi cũng chẳng xoá được lấy một Từ.

Tựa đề của cuốn tiểu thuyết The Moving Finger do Agatha Christie viết và xuất bản năm 1942 được lấy cảm hứng từ bài thơ tứ tuyệt này trong bản dịch Rubaiyat của Omar Khayyam của Edward FitzGerald. Martin Luther King cũng trích dẫn bài tứ tuyệt này của Omar Khayyam trong một bài diễn văn của ông "Beyond Vietnam: A Time to Break Silence" (Bên kia Việt Nam: Thời điểm để Phá vỡ Im lặng):
:"Chúng ta có thể tuyệt vọng cầu xin cho thời gian ngừng trôi trên hành trình của nàng, nhưng thời gian vẫn kiên định với mọi lời khẩn cầu và cứ thế trôi đi. Trên những bộ xương đã tẩy trắng và tàn dư lộn xộn của nhiều nền văn minh là dòng chữ thảm hại, 'Quá muộn màng'. Cuốn sách vô hình của cuộc đời ghi nhận lại một cách trung thực những cảnh giác hay lơ là của chúng ta. Omar Khayyam thật là đúng: 'Ngón tay cứ viết, và mệnh lệnh cứ ban ra.'"

Trong bài diễn văn thứ lỗi cho vụ scandal Clinton-Lewinsky, tổng thống thứ 42 của Hoa Kỳ Bill Clinton cũng trích dẫn bài tứ tuyệt này.